1.11. Локальная теорема Лапласа
Итак, те же независимые испытания, но значения 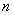 и и 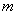 достаточно велики: достаточно велики:
Найти вероятность того, что при 400 бросках монеты орёл выпадет 200 раз.
Очевидно, что здесь следует применить формулу Бернулли, и мы попробуем её применить: 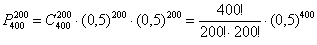 …стоп, что делать дальше? …стоп, что делать дальше?
Микрокалькулятор (по крайне мере, мой) не справился с 400-й степенью и капитулировал перед факториалами.
Воспользуемся стандартной функцией Экселя (БИНОМРАСП – см. п. 3 Калькулятора), которая сумела обработать монстра:
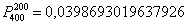 . .
Заостряю ваше внимание, что это точное значение и такое решение вроде бы идеально,… но: 1) программного обеспечения может не оказаться под рукой, 2) учебное решение будет смотреться нестандартно, 3) Эксель – тоже не панацея, «сломался» на значениях, чуть бОльших, чем 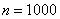 (специально ради интереса ломал). (специально ради интереса ломал).
Возникает мысль написать специальную программу, например, на Паскале, но… сами понимаете, изощрённые фантазии многими преподавателями не одобряются =)
При этом, чем больше 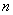 , тем рассчитанная вероятность , тем рассчитанная вероятность 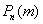 будет лучше приближать точное значению будет лучше приближать точное значению 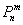 (по Бернулли). Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат (по Бернулли). Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат 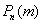 может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность 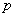 ближе к 0,5, и наоборот – даёт существенную погрешность, когда ближе к 0,5, и наоборот – даёт существенную погрешность, когда 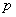 меньше, чем меньше, чем 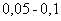 (впрочем, это зависит от (впрочем, это зависит от 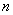 ). Поэтому критерием эффективного использования теоремы является выполнение неравенства ). Поэтому критерием эффективного использования теоремы является выполнение неравенства 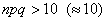 . .
Так, например, если 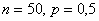 , то , то 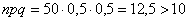 и применение теоремы Лапласа для 50 испытаний оправдано. Но если и применение теоремы Лапласа для 50 испытаний оправдано. Но если 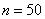 и и 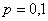 , то , то 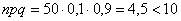 и приближение и приближение 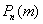 к точному значению к точному значению 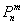 будет плохим. будет плохим.
Оформим официальные отношения с нашим примером:
Задача 75
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно:
а) 200 раз, б) 225 раз.
С чего начать решение? Сначала распишем известные величины, чтобы они были перед глазами:
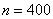 – общее количество независимых испытаний; – общее количество независимых испытаний;
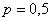 – вероятность выпадения орла в каждом броске; – вероятность выпадения орла в каждом броске;
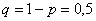 – вероятность выпадения решки. – вероятность выпадения решки.
а) Найдём вероятность того, что в серии из 400 бросков орёл выпадет ровно 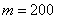 раз. Ввиду большого количества испытаний используем локальную теорему Лапласа: раз. Ввиду большого количества испытаний используем локальную теорему Лапласа: 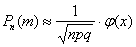 , где , где 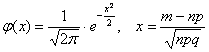 . .
На первом шаге вычислим значение аргумента:
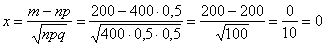
Далее находим соответствующее значение функции: 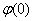 . Это можно сделать несколькими способами. В первую очередь, конечно же, напрашивается прямое вычисление: . Это можно сделать несколькими способами. В первую очередь, конечно же, напрашивается прямое вычисление:
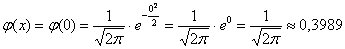 – округление проводят, как правило, до 4 знаков после запятой. Для ускорения вычислений я добавил эту формулу в Калькулятор (пункт 4). – округление проводят, как правило, до 4 знаков после запятой. Для ускорения вычислений я добавил эту формулу в Калькулятор (пункт 4).
Кроме того, существует таблица значений функции 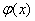 , которая есть практически в любой книге по теории вероятностей. И эта книга не исключение: , которая есть практически в любой книге по теории вероятностей. И эта книга не исключение:
Прямо сейчас откройте Приложение Таблицы
и разберитесь, как пользовать таблицей значений функции 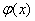 ! !
В частности, найдите по таблице значение 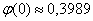 . «Дедовский» способ поможет в тех случаях, когда под рукой не окажется нужной техники (что вполне реально на практике). . «Дедовский» способ поможет в тех случаях, когда под рукой не окажется нужной техники (что вполне реально на практике).
На заключительном этапе применим формулу 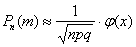 : :
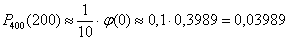 – вероятность того, что при 400 бросках монеты орёл выпадет ровно 200 раз. – вероятность того, что при 400 бросках монеты орёл выпадет ровно 200 раз.
Как видите, полученный результат очень близок к точному значению 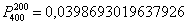 , вычисленному по формуле Бернулли. , вычисленному по формуле Бернулли.
б) Найдём вероятность того, что в серии из 400 испытаний орёл выпадет ровно 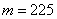 раз. Используем локальную теорему Лапласа. Раз, два, три – и готово: раз. Используем локальную теорему Лапласа. Раз, два, три – и готово:
1) 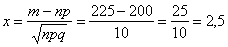
2) 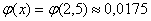
Обязательно найдите это значение по таблице!
3) 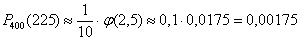 – искомая вероятность. – искомая вероятность.
Ответ: 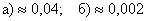
Следующий пример посвящен,… правильно догадываетесь, и это вам для самостоятельного решения :)
Задача 76
Вероятность рождения мальчика равна 0,52. Найти вероятность того, что среди 100 новорожденных окажется ровно: а) 40 мальчиков, б) 50 мальчиков, в) 30 девочек.
Кстати, реальная статистическая вероятность рождения мальчика во многих регионах мира как раз колеблется в пределах от 0,51 до 0,52.
Как вы заметили, вероятности получаются достаточно малыми, и это не должно вводить в заблуждение – ведь речь идёт о вероятностях отдельно взятых, локальных значениях (отсюда и название теоремы). А таковых значений много, и, образно говоря, вероятности «должно хватить на всех». Правда, многие события будут практически невозможными. Так, в серии из 400 испытаний орёл теоретически может выпасть от 0 до 400 раз, и данные события образуют полную группу:
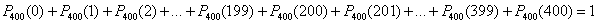
Однако бОльшая часть этих значений представляет собой сущий мизер, и вероятность того, что орёл выпадет ровно 250 раз – уже одна десятимиллионная: 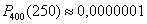 . О значениях вроде . О значениях вроде  тактично умолчим :) тактично умолчим :)
С другой стороны, не следует недооценивать и «скромные результаты»: так, если 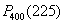 составляет всего около составляет всего около 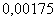 , то вероятность того, орёл выпадет, скажем, от 220 до 250 раз, будет весьма заметна. А теперь задумаемся: как найти эту вероятность? С современными вычислительными возможностями не составит труда воспользоваться теоремой сложения вероятностей несовместных событий и вычислить сумму , то вероятность того, орёл выпадет, скажем, от 220 до 250 раз, будет весьма заметна. А теперь задумаемся: как найти эту вероятность? С современными вычислительными возможностями не составит труда воспользоваться теоремой сложения вероятностей несовместных событий и вычислить сумму 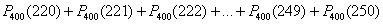 либо абсолютно точное значение через формулу Бернулли: либо абсолютно точное значение через формулу Бернулли: 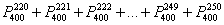 . .
Но гораздо проще эти значения объединить. А объединение чего-либо называется интегрированием:
 1.12. Интегральная теорема Лапласа 1.12. Интегральная теорема Лапласа
 1.10. Формула Пуассона 1.10. Формула Пуассона
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!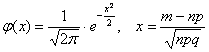 .
. 1.12. Интегральная теорема Лапласа
1.12. Интегральная теорема Лапласа  1.10. Формула Пуассона
1.10. Формула Пуассона