1.12. Интегральная теорема Лапласа
Как и в локальной теореме, количество испытаний 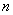 должно быть достаточно большими вероятность должно быть достаточно большими вероятность 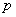 не слишком мала, и на практике следует ориентироваться на
выполнение того же неравенства не слишком мала, и на практике следует ориентироваться на
выполнение того же неравенства 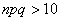 , в
противном случае приближение к точному результату , в
противном случае приближение к точному результату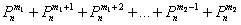 (полученному по Бернулли) будет плохим. (полученному по Бернулли) будет плохим.
Задача 77
Вероятность поражения стрелком мишени равна 0,7. Найти вероятность того, что при 100 выстрелах мишень будет поражена:
а) от 60 до 80 раз, б) не менее 65 раз
Решение: в данной задаче речь идёт о повторных независимых
испытаниях, причём их количество 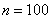 достаточно велико. Вероятность попадания в цель при каждом выстреле составляет достаточно велико. Вероятность попадания в цель при каждом выстреле составляет
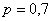 , следовательно, вероятность промаха: , следовательно, вероятность промаха: 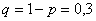 . .
Оценим эффективность применения интегральной теоремы Лапласа:
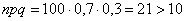 , значит, теорема Лапласа даст хорошее
приближение. , значит, теорема Лапласа даст хорошее
приближение.
а) Найдём вероятность 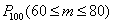 – того, что при 100 выстрелах мишень будет поражена от – того, что при 100 выстрелах мишень будет поражена от 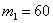 до до 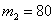 раз. Используем интегральную теорему Лапласа: раз. Используем интегральную теорему Лапласа:
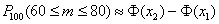 , где , где 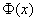 – функция Лапласа. – функция Лапласа.
Сначала вычислим значения аргументов:
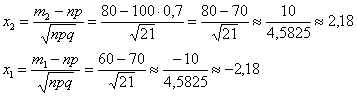
Обращаю внимание, что произведение 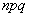 не
обязано извлекаться из-под корня нацело (как любят «подгонять» числа авторы задач) – без тени сомнения извлекаем корень
приближённо и округляем результат; я привык оставлять 4 знака после запятой. не
обязано извлекаться из-под корня нацело (как любят «подгонять» числа авторы задач) – без тени сомнения извлекаем корень
приближённо и округляем результат; я привык оставлять 4 знака после запятой.
А вот полученные значения 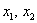 обычно
округляют до 2 знаков – эта традиция идёт из таблицы значений функции обычно
округляют до 2 знаков – эта традиция идёт из таблицы значений функции 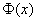 (см. Приложение Таблицы), где аргументы
представлены именно в таком виде. (см. Приложение Таблицы), где аргументы
представлены именно в таком виде.
Таким образом:
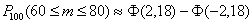
Как вычислить значения функции 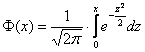 ?
Ручные вычисления и микрокалькулятор здесь не помогут, поскольку этот интеграл не берётся. Но вот в Экселе соответствующий функционал есть
– используйте Пункт 5 Калькулятора. ?
Ручные вычисления и микрокалькулятор здесь не помогут, поскольку этот интеграл не берётся. Но вот в Экселе соответствующий функционал есть
– используйте Пункт 5 Калькулятора.
Кроме того, ОБЯЗАТЕЛЬНО найдите значение 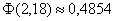 в таблице! в таблице!
И, учитывая нечётность функции Лапласа 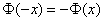 , получаем, распишу подробно: , получаем, распишу подробно:
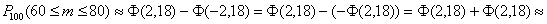
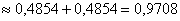 – вероятность того, что при 100
выстрелах мишень будет поражена от 60 до 80 раз. – вероятность того, что при 100
выстрелах мишень будет поражена от 60 до 80 раз.
Результат чаще всего округляют до 4 знаков после запятой (опять же в соответствии с форматом таблицы).
б) Найдём вероятность того, что при 100 выстрелах мишень будет поражена не менее 65 раз. Это означает, что
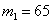 , а , а 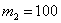 . .
Вычислим значения аргументов:
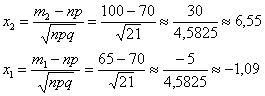
Таким образом, по интегральной теореме Лапласа и таблице значений функции Лапласа (лучше использовать такую формулировку!),
получаем:
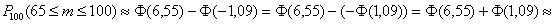
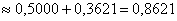 – вероятность того, что при 100
выстрелах мишень будет поражена не менее 65 раз. – вероятность того, что при 100
выстрелах мишень будет поражена не менее 65 раз.
Примечание: начиная с 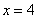 , можно
считать, что , можно
считать, что 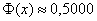 , или, если записать строже: , или, если записать строже:
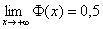 . .
Ответ: а) 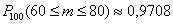 , б) , б)
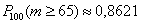
И ради исследовательского интереса я вычислил более точные значения с помощью формулы Бернулли («протянув» в Экселе формулу БИНОМРАСП):
 
– как видите, расхождение получилось существенным, это обусловлено небольшим значением 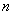 . А ещё, надо признать, рассматриваемый метод устарел, ибо экселевские
расчёты отняли у меня буквально минуту. Но мы отнесёмся к этому с пониманием, таки Пьер-Симон маркиз де Сад Лаплас жил в 18-19 веках J . А ещё, надо признать, рассматриваемый метод устарел, ибо экселевские
расчёты отняли у меня буквально минуту. Но мы отнесёмся к этому с пониманием, таки Пьер-Симон маркиз де Сад Лаплас жил в 18-19 веках J
Следующая задача для самостоятельного решения:
Задача 78
В здании имеется 2500 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что вечером будет
включено:
а) половина ламп,
б) не менее 1250 и не более 1275 ламп,
в) не более 1000 ламп
Примерный образец чистового оформления решения в конце книги.
Следует отметить, что рассматриваемые задачи очень часто встречаются в «обезличенном» виде, примерно таком:
Производится некоторый опыт, в котором случайное событие 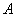 может появиться с вероятностью 0,5. Опыт повторяется в неизменных условиях
2500 раз. Определить вероятность того, что в 2500 опытах событие может появиться с вероятностью 0,5. Опыт повторяется в неизменных условиях
2500 раз. Определить вероятность того, что в 2500 опытах событие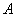 произойдет от 1250 до 1275 раз. произойдет от 1250 до 1275 раз.
 1.13. Относительная частота события и статистическая вероятность 1.13. Относительная частота события и статистическая вероятность
 1.11. Локальная теорема Лапласа 1.11. Локальная теорема Лапласа
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!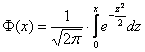 – функция Лапласа,
– функция Лапласа, 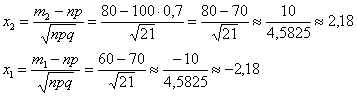
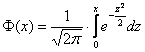 ?
Ручные вычисления и микрокалькулятор здесь не помогут, поскольку этот интеграл не берётся. Но вот в Экселе соответствующий функционал есть
– используйте Пункт 5 Калькулятора.
?
Ручные вычисления и микрокалькулятор здесь не помогут, поскольку этот интеграл не берётся. Но вот в Экселе соответствующий функционал есть
– используйте Пункт 5 Калькулятора. 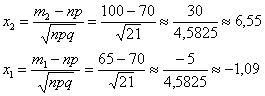
 1.13. Относительная частота события и статистическая вероятность
1.13. Относительная частота события и статистическая вероятность  1.11. Локальная теорема Лапласа
1.11. Локальная теорема Лапласа