|
Ваш репетитор, справочник и друг!
|
1.13. Относительная частота события и статистическая вероятностьДавайте вспомним, с чего всё начиналось: Вероятность наступления события
Например: Внимательный читатель заметил, что все комментарии о вероятностях сформулированы в будущем времени. И это не
случайность – классическое определение оценивает вероятность ДО
проведения испытаний и даже без их фактического проведения. То есть, монета ещё не подброшена, а вероятность появления
орла мы уже знаем. Можно дать зарок никогда не брать в руки кубик либо колоду карт, однако, вероятности событий Почему такое возможно? Такое возможно потому, что все элементарные исходы известны и подсчитаны заранее: орёл и решка – итого 2 элементарных исхода; Кроме того, для применения классического определения вероятности необходима равновозможность элементарных исходов (см. определение). Равновозможность выпадения граней монеты либо кубика обуславливается симметрией и несмещённым центром тяжести, колода же карт должна быть полной, некраплёной и хорошо перемешанной. И всё было бы ладно, но в реальной жизни рассмотренные выше модели встречаются нечасто. В большинстве ситуаций элементарные исходы перечислить затруднительно или невозможно, и ещё труднее обосновать их равновозможность. Простой пример: Штирлиц пошёл в лес за грибами. Найти вероятность того, что он найдёт подберёзовик. Совершенно понятно, что все грибы в лесу (общее количество элементарных исходов) пересчитать практически невозможно, а значит, классическое определение вероятности не срабатывает. И даже если группа разведчиков учтёт все грибы в небольшой роще, классифицирует их по видам, то препятствием станет неравновозможность исходов. Почему? Поляна мухоморов намного заметнее, чем замаскировавшиеся подберёзовики…, так, кто это предложил их покрасить в красный цвет? :) …ну что тут сказать? – с такими страна на пропадёт! Кстати, вспомнилась ещё одна каверзная задачка на счёт неравновозможности исходов. Её суть состоит в следующем: если в городе
проживает примерно равное количество мужчин и женщин (которых подсчитать значительно проще =)), то это ещё не значит, что
вероятность встретить на улице мужчину либо женщину равна А теперь вновь обратим внимание на шаблонные формулировки стандартных задач тервера: «Стрелок попадает в мишень с вероятностью 0,8»; Возникает вопрос, откуда взялись эти значения? И ответ здесь один: данные вероятности могли получиться только на основе ранее проведённых опытов. Относительной частотой события Относительная частота наряду с вероятностью является одним из ключевых понятий тервера, но если классическое либо геометрическое определение вероятности не требуют проведения испытаний, то относительная частота рассчитывается ПОСЛЕ опытов и исключительно на основе фактически полученных данных. В том случае, если серии испытаний проводятся в неизменных условиях, то относительная частота обнаруживает свойство устойчивости, то есть колеблется около определённого значения. Поясню это на конкретных примерах: Пусть некий профессиональный стрелок произвёл 100 выстрелов по мишени и попал 83 раза. Тогда относительная частота поражения цели
составит: Предположим, что тот же самый стрелок в точно такой же «форме» и в приблизительно таких же условиях снова провёл серию из 100
выстрелов. Вероятно ли, что он снова попадёт 83 раза? Не очень. Но количество попаданий вряд ли будет сильно отличаться от предыдущего
результата. Пусть, например, стрелок попал 79 раз. Тогда относительная частота поражения цели составит: Иногда будут случаться блестящие серии более 90 попаданий, иногда «провалы», но среднее количество попаданий будет варьироваться около 80. И когда количество фактически проведённых испытаний станет достаточно большим, то речь зайдёт о статистической вероятности. Если в одинаковых (примерно одинаковых) условиях проведено достаточно много испытаний, то за статистическую вероятность события принимают относительную частоту данного события либо близкое число. Предположим, что на протяжении нескольких лет наш спортсмен, сохраняя стабильный уровень подготовки, совершил 10000 выстрелов и попал
8037 раз. Относительная частота поражения цели составит: Именно так и собирается богатая спортивная статистика в различных видах спорта. Аналогичная история с утверждением «Вероятность изготовления бракованной детали на данном станке равна 0,05». Эту оценку невозможно получить с помощью классического определения вероятности –
она следует только из практики! Если на станке произведены десятки тысяч деталей и на каждую, скажем, тысячу выпущенных деталей,
приходится в среднем 50 бракованных, то в качестве статистической вероятности брака принимается значения В Задаче 76 фигурировала вероятность рождения мальчика В учебном пособии В.Е. Гмурмана есть весьма удачный пример, в котором продемонстрировано, как при подбрасывании монеты
относительная частота появления орла приближается к своей вероятности
Таким образом, с увеличением количества независимых испытаний Вернёмся к рулетке. В отдельно взятом сеансе игры отдельно взятый человек может выиграть, причём выиграть по-крупному. Это случайность. Но, совершая миллионы и миллионы оборотов, рулетка на протяжении веков приносит неизменную прибыль владельцам казино. И это закономерность. Существует байка о том, что крупный выигрыш не отдадут, а если и отдадут, то «вы с ним не дойдёте до дома». Чисто житейская фантазия. Да, кому-то повезло, но сколько проиграется?! К тому же человек, посещающий подобные заведения, с большой вероятностью придёт снова и «сольёт» ещё больше. А чтобы он вернулся, казино, скорее наоборот – создаст максимальный комфорт и безопасность для «счастливчика». Ибо на длинной дистанции разорятся ВСЕ игроки. Другой пример. Пусть в некой лотерее приняло участие Организатор лотереи знает, что из миллиона проданных билетов выиграют около 300 тысяч с небольшим отклонением. Этот факт важен для
грамотного распределения призового фонда, и это закономерность. Но всем участникам лотереи достаётся….
А если учесть тот факт, что львиная доля выигрышей – сущая мелочь, то картина вырисовывается совсем унылая. Ситуацию спасают красочные телевизионные розыгрыши и различные психологические трюки. Желающие могут самостоятельно исследовать вероятность выигрыша в различные лотереи – вся статистика есть в свободном доступе ;) И, говоря откровенно, вас просто поразит это чудовищное надувательство. Впрочем, рулетка гораздо коварнее. Практическая часть параграфа будет тесно связана с только что изложенным материалом: Вероятность отклонения относительной частоты от вероятности Вероятность того, что в Эта формула следует из интегральной теоремы Лапласа. Итак, расклад следующий: в распоряжении имеется вероятность Требуется найти вероятность того, что в серии из Возвращаемся к любимой задаче: Задача 79 Решение: используем формулу По условию,
Напоминаю, что значения функции Лапласа можно найти по соответствующей таблице или с помощью Калькулятора (Пункт 5). Ответ: И на самом деле рассмотренная задача эквивалентна следующей: «Найти вероятность того, что среди 1000 новорожденных будет от 500 до 540 мальчиков, если вероятность рождения мальчика равна 0,52». А эта задача как раз и решается через разобранную выше интегральную теорему Лапласа. Следующая задача для самостоятельного решения: Задача 80 Условие сформулировано в общем виде, как оно чаще всего и бывает. Ещё раз повторим суть задания: проводится Для Решение: используем ту же формулу По условию, требуется найти такое количество опытов По таблице значений функции Возведём обе части в квадрат: Ответ: для того, чтобы с вероятностью большей, чем 0,9, можно было ожидать отклонения
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!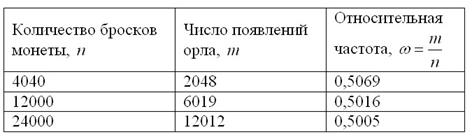
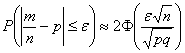 , где
, где 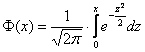 – функция Лапласа.
– функция Лапласа.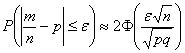
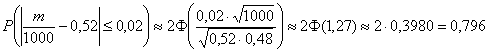 – искомая вероятность.
– искомая вероятность. 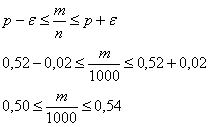
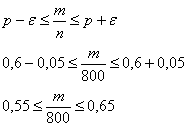
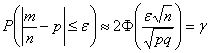 , но на этот раз нам известны величины:
, но на этот раз нам известны величины: 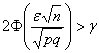 – подставляем известные значения
и делим обе части на два:
– подставляем известные значения
и делим обе части на два: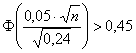
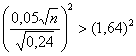
 2.1. Случайные величины
2.1. Случайные величины  1.12. Интегральная теорема Лапласа
1.12. Интегральная теорема Лапласа