Ваш репетитор, справочник и друг!

Практикум по теории вероятностей

Научись решать в считанные дни!

2.2.1. Закон распределения дискретной случайной величины

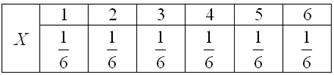
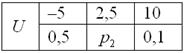
Закон распределения дискретной случайной величины – это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:

Довольно часто встречается термин ряд распределения, но в некоторых контекстах он звучит двусмысленно, и поэтому я буду использовать слово закон.

И сразу очень важный момент: поскольку случайная величина обязательно примет одно из значений , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:

или, если записать свёрнуто:

Справка: – это значок суммирования, а – переменная-«счётчик», которая «пробегает» все значения от 1 до .

Так, например, закон распределения выпавших на кубике очков имеет следующий вид:

…как говорится, без комментариев.
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:

Задача 82
Пусть некая игра имеет следующий закон распределения выигрыша:

(в 1-й строке размер выигрыша в условных единицах, а во 2-й – его вероятность)

Найти .

Решение: так как случайная величина может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:

Разоблачаем «партизана»:

– таким образом, вероятность выигрыша условных единиц составляет 0,4.

Контроль: , в чём и требовалось убедиться.

Ответ:

Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы сложения / умножения вероятностей и другие фишки:

Задача 83
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины – размера выигрыша, если из коробки наугад извлекается один билет.

Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно рублей. Всего таковых билетов 50 – 12 = 38, и по классическому определению:
– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.

С остальными случаями всё просто. Вероятность выигрыша рублей составляет:
И для :

Проверка: – и это особенно приятный момент таких заданий.

Ответ: искомый закон распределения выигрыша:

Следующее задание для самостоятельного решения:

Задача 84
Вероятность того, что стрелок поразит в мишень, равна . Составить закон распределения случайной величины – количества попаданий после 2 выстрелов.

Вспоминаем теоремы умножения и сложения! Решение и ответ в конце книги.

Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики:

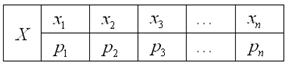
2.2.2. Математическое ожидание дискретной случайной величины

2.1. Случайные величины

| Оглавление |

Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти после Оглавления.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин