2.4.1. Непрерывная случайная величина и её функция распределения

В отличие от дискретной случайной величины, НСВ может принять любое действительное значение из некоторого промежутка ненулевой длины, что делает невозможным её представление в виде таблицы (т.к. действительных чисел несчётно много). И посему непрерывную случайную величину задают функциями двух типов:

1) функцией распределения ,

2) функцией плотности распределения .

Начнём с функции распределения.

Как отмечалось ранее, функция распределения непрерывной случайной величины определяется точно так же, как и в дискретном случае, повторим определение:

– вероятность того, что случайная величина примет значение, МЕНЬШЕЕ, чем переменная , которая «пробегает» все действительные значения от «минус» до «плюс» бесконечности.

С увеличением функция распределения «накапливает» (суммирует) вероятности, а значит, является неубывающей и изменяется в пределах . По этой причине её также называют интегральной функцией распределения.

Важной особенностью непрерывного случая является тот факт, что функция распределения ЛЮБОЙ непрерывной случайной величины всюду непрерывна! Часто её можно встретить в кусочном виде, например:

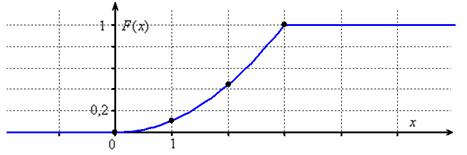
однако в точках «стыка» всё хорошо:

и если там разрыв, то вы имеете дело с опечаткой или откровенной ошибкой!

! Носама по себе непрерывность и ноль слева, единица справа – ещё не означают, что перед нами функция распределения.

При ручном построении чертежа целесообразно найти опорные точки; в нашем примере удобно взять: и плавно-плавно провести карандашом кусочек параболы :

Напоминаю, что левый нижний луч следует прочертить жирно (чтобы он не сливался с осью), а правый верхний луч продолжить за остриё оси (т.к. график бесконечен). Функция распределения не можетубывать, и если вдруг окажется, что какой-то кусок графика идёт «сверху вниз», то ищите ошибку или опять же – имеет место опечатка. А может просто дрогнула рука :)

Что касаемо масштаба, то смотрим по ситуации, чаще всего оптимальный масштаб составляет 1 ед. = 1 см (две клетки), но поскольку я строю графики не от руки, то особо не слежу за пропорциями – в данном случае по оси ординат вышло примерно в 2 раза больше, чем по оси абсцисс.

Теперь вернёмся к смыслу функции распределения и рассмотрим пару конкретных значений :

– вероятность того, что случайная величина примет значение, МЕНЬШЕЕ, чем ;

– вероятность того, что случайная величина примет значение, МЕНЬШЕЕ, чем .

Ну и очевидно, что рассматриваемая случайная величина принимает случайные, наперёд неизвестные значения из отрезка . Если вкладывать в задачу содержательный смысл, то это может быть случайная продолжительность некоего процесса (в секундах, например), или масса либо размер случайно выбранного объекта (например, плюшевого мишки). И так далее, примеров – масса. Конкретные задачи обязательно рассмотрим, но прежде мы остановимся на технической стороне вопроса.

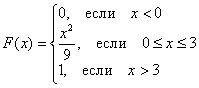
2.4.2. Вероятность попадания в промежуток

2.3.4. Гипергеометрическое распределение вероятностей

| Оглавление |

Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти после Оглавления.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин