2.4.2. Вероятность попадания в промежуток
Вероятность того, что случайная величина примет значение из некоторого промежутка рассчитывается ещё проще, чем для дискретной случайной величины. Здесь нет никакой Санта-Барбары: отрезок ли 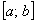 нам дан, полуинтервал нам дан, полуинтервал 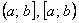 или интервал или интервал 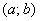 , соответствующую вероятность можно вычислить по единой формуле: , соответствующую вероятность можно вычислить по единой формуле:
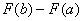 , и в следующем параграфе мы обоснуем это утверждение. , и в следующем параграфе мы обоснуем это утверждение.
Например:
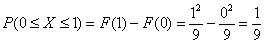 – вероятность того, что случайная величина примет какое-либо значение из отрезка – вероятность того, что случайная величина примет какое-либо значение из отрезка 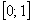 . И точно такими ми же будут вероятности . И точно такими ми же будут вероятности 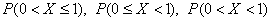 (скоро будет понятно, почему). (скоро будет понятно, почему).
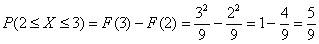 – вероятность того, что случайная величина примет значение из отрезка – вероятность того, что случайная величина примет значение из отрезка 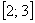 ; ;
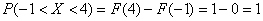 – вероятность того, что случайная величина примет значение из интервала – вероятность того, что случайная величина примет значение из интервала 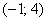 ; ;
и так далее.
Наверное, вы заметили, что на участках одинаковой длины результаты получились разными: 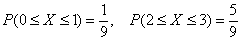 . И возникает вопрос: как оценить «концентрацию» вероятностей на различных промежутках? – ведь функция распределения . И возникает вопрос: как оценить «концентрацию» вероятностей на различных промежутках? – ведь функция распределения 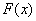 характеризует накопление вероятностей по мере увеличения характеризует накопление вероятностей по мере увеличения 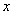 , и каждый раз вычислять , и каждый раз вычислять 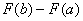 что-то неохота. что-то неохота.
Эффективный ответ на поставленный вопрос даёт:
 2.4.3. Функция ПЛОТНОСТИ распределения вероятностей 2.4.3. Функция ПЛОТНОСТИ распределения вероятностей
 2.4.1. Функция распределения непрерывной случайной величины 2.4.1. Функция распределения непрерывной случайной величины
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни! 2.4.3. Функция ПЛОТНОСТИ распределения вероятностей
2.4.3. Функция ПЛОТНОСТИ распределения вероятностей 2.4.1. Функция распределения непрерывной случайной величины
2.4.1. Функция распределения непрерывной случайной величины