|
Ваш репетитор, справочник и друг!
|
5.5.5. Пересекающиеся прямые в пространствеПересекающиеся прямые пространства обязательно лежат в одной плоскости, причём их направляющие векторы неколлинеарны: Первая мысль – всеми силами навалиться на точку пересечения И тут сразу же подумалось, зачем себе отказывать в правильных желаниях?! Давайте навалимся на неё прямо сейчас! Как найти точку пересечения пространственных прямых?Собственно: Задача 156 Найти точку пересечения прямых Решение: Перепишем уравнения прямых в параметрической форме: Приём решения стандартен и уже встречался, когда мы вымучивали уравнения общего перпендикуляра скрещивающихся прямых. Точка пересечения прямых Но эта же точка принадлежит и второй прямой, следовательно, существует значение Приравниваем соответствующие уравнения и проводим упрощения: Получена система трёх линейных уравнений с двумя неизвестными, которую опять же решим «школьным» способом. Из 1-го уравнения выразим В результате получилась совместная система, из которой следует, что Подставим найденное значение параметра Ответ: Теперь рассмотрим особый случай пересечения прямых:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»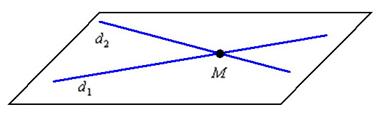
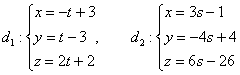
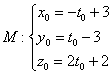
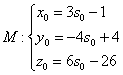
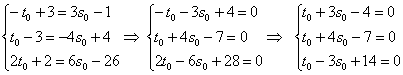
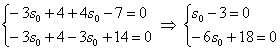
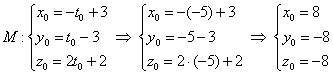 , и для проверки подставим значение
, и для проверки подставим значение 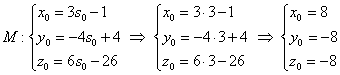
 5.5.6. Как найти прямую, перпендикулярную данной?
5.5.6. Как найти прямую, перпендикулярную данной? 5.5.4. Как найти расстояние между скрещивающимися прямыми?
5.5.4. Как найти расстояние между скрещивающимися прямыми?