|
Ваш репетитор, справочник и друг!
|
5.5.6. Как найти прямую, перпендикулярную данной?Обращаю внимание, что для скрещивающихся прямых таких прямых можно провести бесконечно много, а вот для пересекающихся – задача имеет единственное решение: Задача 157 а) Составить уравнения прямой, проходящей через точку б) Найти расстояние от точки а) Решение: обозначим неизвестную прямую через И начинаем раскручивать задачу: что нам известно об этой прямой? Известна её точка План есть, и мы счастливы: 1) Вытащим из уравнений прямой «эль» её направляющий вектор И вот уже в третий раз используем тот же самый фокус. Рассмотрим точку Тогда: 2) По условию прямые должны быть перпендикулярны, следовательно, их направляющие векторы Что получилось? Простейшее линейное уравнение с одной неизвестной: 3) Значение параметра известно, находим точку: И направляющий вектор: 4) Уравнения прямой Ответ: Но, разумеется, тут можно было взять и вектор Проверка состоит из двух этапов: 1) проверяем направляющие векторы прямых на ортогональность; 2) подставляем координаты точки Об этих действиях говорилось много, поэтому я выполнил проверку на черновике.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»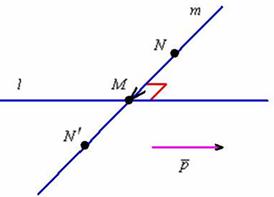
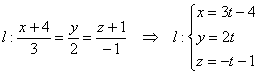
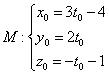 , или в строчку:
, или в строчку: 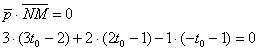
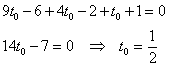
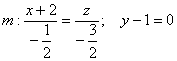
 5.5.7. Как найти расстояние от точки до прямой?
5.5.7. Как найти расстояние от точки до прямой? 5.5.5. Пересекающиеся прямые в пространстве
5.5.5. Пересекающиеся прямые в пространстве