|
Ваш репетитор, справочник и друг!
|
5.5.7. Как найти расстояние от точки до прямой?б) Решение: Найдём расстояние от точки Способ первый. Данное расстояние в точности равно длине перпендикуляра Способ второй. В практических задачах основание перпендикуляра Но здесь тоже придётся потрудиться: 1) Из уравнений прямой 2) Точка 3) Найдём векторное произведение и вычислим его длину: 4) Таким образом, искомое расстояние: Ответ:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»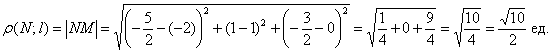
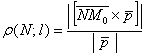 , где
, где 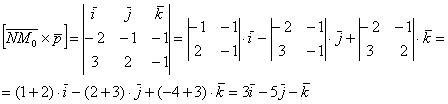
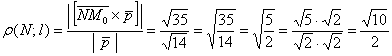
 5.5.8. Как найти точку, симметричную относительно прямой?
5.5.8. Как найти точку, симметричную относительно прямой? 5.5.6. Как найти прямую, перпендикулярную данной?
5.5.6. Как найти прямую, перпендикулярную данной?