6.4. Коническая поверхность
Каноническое уравнение 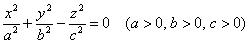 задаёт коническую поверхность или, если короче, конус. Но это опять же не совсем тот конус, который всем знаком со времён далёкого детства. задаёт коническую поверхность или, если короче, конус. Но это опять же не совсем тот конус, который всем знаком со времён далёкого детства.
Форму многих поверхностей удобно исследовать методом сечений, который я потихоньку начал использовать в предыдущих параграфах. Суть метода состоит в том, что мы «рассекаем пациентов» плоскостями, и получившиеся сечения позволяют нам хорошо понять, как выглядит та или иная поверхность.
Перепишем уравнение в виде 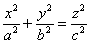 и исследуем сечения конуса плоскостями и исследуем сечения конуса плоскостями 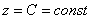 , параллельными плоскости , параллельными плоскости 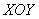 . Подставим . Подставим 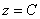 в уравнение конической поверхности: в уравнение конической поверхности: 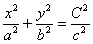 . .
Очевидно, что случаю 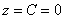 соответствует уравнение соответствует уравнение 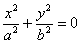 , задающее пару мнимых пересекающихся прямых с единственной действительной точкой пересечения в начале координат. Данная точка называется вершиной конуса. , задающее пару мнимых пересекающихся прямых с единственной действительной точкой пересечения в начале координат. Данная точка называется вершиной конуса.
Если же 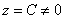 , то уравнение , то уравнение 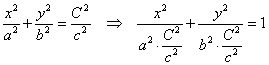 задаёт эллипсы различных размеров, причём из последнего уравнения хорошо видно, что с увеличением абсолютного значения задаёт эллипсы различных размеров, причём из последнего уравнения хорошо видно, что с увеличением абсолютного значения 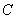 полуоси эллипсов неограниченно растут. Таким образом, коническая поверхность бесконечна: полуоси эллипсов неограниченно растут. Таким образом, коническая поверхность бесконечна:
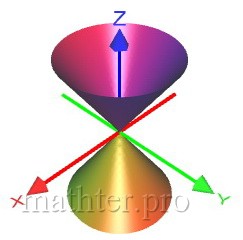
Если коническую поверхность «разрезать» любой плоскостью 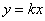 , проходящей через ось , проходящей через ось 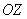 , то каждое такое сечение будет представлять собой две пересекающиеся прямые, лежащие в плоскости , то каждое такое сечение будет представлять собой две пересекающиеся прямые, лежащие в плоскости 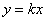 и проходящие через начало координат. Множество всех этих прямых, собственно, и образуют коническую поверхность. И логично, что каждая такая прямая называется образующей конуса. и проходящие через начало координат. Множество всех этих прямых, собственно, и образуют коническую поверхность. И логично, что каждая такая прямая называется образующей конуса.
На практике почти всегда приходится иметь дело с упрощенной версией конуса, когда сечения плоскостями 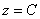 представляют собой окружности. Такой конус называют конусом вращения, и во многих практических задачах его легко определить по следующему уравнению: представляют собой окружности. Такой конус называют конусом вращения, и во многих практических задачах его легко определить по следующему уравнению:
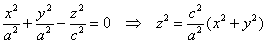 – с «зет» в левой части и равными коэффициентами при – с «зет» в левой части и равными коэффициентами при 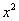 и и 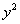 . Как вы правильно догадались, функция . Как вы правильно догадались, функция 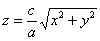 задаёт верхнюю часть конуса, а функция задаёт верхнюю часть конуса, а функция 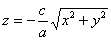 – его нижнюю часть. – его нижнюю часть.
Познавательная вариация по теме:
Задача 176
Построить поверхность 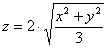
Решение: уравнение имеет вид 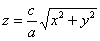 и определяет половину конуса, располагающуюся в верхнем полупространстве. Вершина конической поверхности, понятно, расположена в начале координат, но как построить всё остальное? и определяет половину конуса, располагающуюся в верхнем полупространстве. Вершина конической поверхности, понятно, расположена в начале координат, но как построить всё остальное?
Возведём обе части исходного уравнения в квадрат:
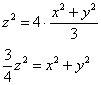
Далее выберем небольшое положительное значение «зет», например, 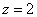 и найдём линию пересечения этой плоскости с нашей поверхностью: и найдём линию пересечения этой плоскости с нашей поверхностью:
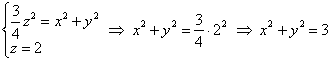 – окружность радиуса – окружность радиуса 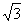 . .
Теперь на высоте 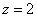 изобразим окружность изобразим окружность 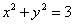 и аккуратно проведём 4 образующие конуса: и аккуратно проведём 4 образующие конуса:
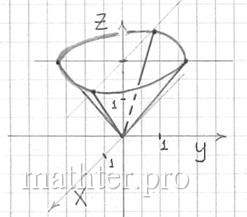 Образующие, в принципе, можно было продолжить и выше плоскости 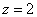 . .
Но не ниже плоскости 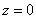 ! – Не забываем, что уравнение ! – Не забываем, что уравнение 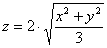 задаёт только верхнюю часть поверхности и поэтому никаких «хвостиков» в нижнем полупространстве быть не должно. задаёт только верхнюю часть поверхности и поэтому никаких «хвостиков» в нижнем полупространстве быть не должно.
Пожалуй, простейшая коническая поверхность для самостоятельного изучения:
Задача 177
Построить коническую поверхность 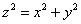 . Записать неравенства, определяющие внутреннюю и внешнюю часть конуса. . Записать неравенства, определяющие внутреннюю и внешнюю часть конуса.
В образце решения изображён фрагмент конуса, расположенный между плоскостями 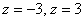 . Ну, а с неравенствами, думаю, сообразите самостоятельно. В случае мучительных сомнений всегда можно взять точку (внутри или снаружи конуса) и проверить, удовлетворяют ли её координаты неравенству. . Ну, а с неравенствами, думаю, сообразите самостоятельно. В случае мучительных сомнений всегда можно взять точку (внутри или снаружи конуса) и проверить, удовлетворяют ли её координаты неравенству.
Переходим к следующему семейству:
 6.5. Параболоиды 6.5. Параболоиды
 6.3. Эллипсоид 6.3. Эллипсоид
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»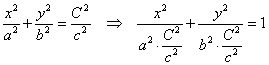 задаёт
задаёт
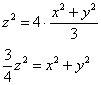
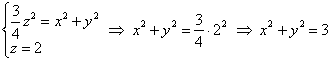 – окружность радиуса
– окружность радиуса 
 6.5. Параболоиды
6.5. Параболоиды 6.3. Эллипсоид
6.3. Эллипсоид