6.5. Параболоиды
Их два. Сначала рассмотрим мегапопулярный
Эллиптический параболоид
Каноничный эллиптический параболоид задаётся уравнением (система координат, напоминаю, везде декартова) 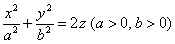 . Данная поверхность выглядит бесконечной чашей: . Данная поверхность выглядит бесконечной чашей:
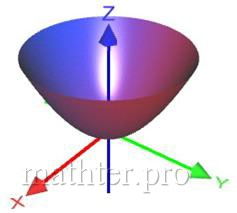 Название «эллиптический параболоид» тоже произошло из результатов исследования сечений. В горизонтальных сечениях плоскостями Название «эллиптический параболоид» тоже произошло из результатов исследования сечений. В горизонтальных сечениях плоскостями 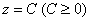 получаются различные эллипсы: получаются различные эллипсы:
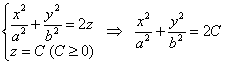 , в частности, при , в частности, при 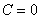 эллипс вырождается в точку (начало координат), которая называется вершиной эллиптического параболоида. эллипс вырождается в точку (начало координат), которая называется вершиной эллиптического параболоида.
А вертикальные сечения плоскостями, параллельными оси 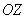 , представляют собой различные параболы. Например, сечение координатной плоскостью , представляют собой различные параболы. Например, сечение координатной плоскостью 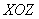 : :
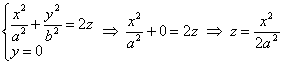 – парабола, лежащая в плоскости – парабола, лежащая в плоскости 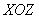 . .
и сечение плоскостью 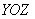 : :
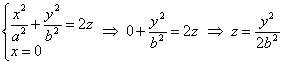 – парабола, лежащая в плоскости – парабола, лежащая в плоскости 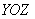 . .
Отсюда и эллиптический параболоид.
На практике обычно встречается упрощенная версия поверхности с горизонтальными сечениями-окружностями. Перепишем каноническое уравнение в прикладном функциональном виде: 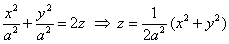 – характерным признаком этой функции, как и в ситуации с конусом, является равенство коэффициентов при – характерным признаком этой функции, как и в ситуации с конусом, является равенство коэффициентов при 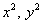 . .
Задача 178
Построить поверхность 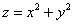 . Записать неравенства, определяющие внутреннюю и внешнюю часть эллиптического параболоида. . Записать неравенства, определяющие внутреннюю и внешнюю часть эллиптического параболоида.
Решение: используем ту же методику, что и при построении конической поверхности. Рассмотрим какое-нибудь не очень большое значение «зет», здесь удобно выбрать 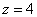 , и найдём сечение эллиптического параболоида этой плоскостью: , и найдём сечение эллиптического параболоида этой плоскостью:
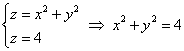 – окружность радиуса 2. – окружность радиуса 2.
Теперь на высоте 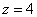 изобразим данную окружность и аккуратно соединим её с вершиной (началом координат) двумя параболами. В результате получится такая вот симпатичная чашка: изобразим данную окружность и аккуратно соединим её с вершиной (началом координат) двумя параболами. В результате получится такая вот симпатичная чашка:
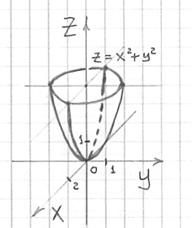
Рассматриваемый частный случай параболоида с сечениями-окружностями называют параболоидом вращения, поскольку его можно получить вращением параболы вокруг оси 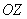
С неравенствами ничего нового. Нетрудно догадаться, что неравенство 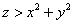 или, если развернуть запись в более привычном порядке, или, если развернуть запись в более привычном порядке, 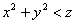 определяет множество точек внутри чаши (т.к. неравенство строгое, то сама поверхность не входит в решение). И, соответственно, неравенство определяет множество точек внутри чаши (т.к. неравенство строгое, то сама поверхность не входит в решение). И, соответственно, неравенство 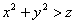 задаёт множество внешних точек. задаёт множество внешних точек.
По моим наблюдениям, на практике часто встречается эллиптический параболоид вида 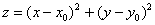 , который выглядит точно так же, но мигрировал вершиной в точку , который выглядит точно так же, но мигрировал вершиной в точку 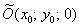 . .
Ещё одно типичное расположение эллиптического параболоида:
Задача 179
Построить поверхность 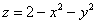
Решение: если коэффициенты при 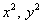 отрицательны (сразу оба), то чаша параболоида «смотрит вниз». Вершина поверхности расположена в точке отрицательны (сразу оба), то чаша параболоида «смотрит вниз». Вершина поверхности расположена в точке 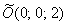 . Это понятно не только интуитивно, но и подкрепляется простым аналитическим рассуждением: очевидно, что, рассмотрев любую другую пару значений . Это понятно не только интуитивно, но и подкрепляется простым аналитическим рассуждением: очевидно, что, рассмотрев любую другую пару значений 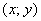 , мы уменьшим функцию , мы уменьшим функцию 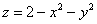 . Таким образом, точка . Таким образом, точка 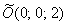 – это самая высокая точка (максимум). – это самая высокая точка (максимум).
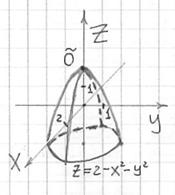 В целях построения поверхность удобно «отсечь» плоскостью 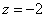 . Сечение представляет собой: . Сечение представляет собой:
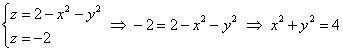 – окружность радиуса 2. – окружность радиуса 2.
Отмечаем точку 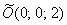 , проводим окружность , проводим окружность 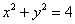 на высоте на высоте 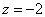 и аккуратно завершаем конструкцию 4 направляющими (ветвями параболы). и аккуратно завершаем конструкцию 4 направляющими (ветвями параболы).
Творческое задание для самостоятельного решения:
Задача 180
Построить эллиптический параболоид 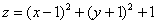
Теперь менее распространённый «собрат»:
Гиперболический параболоид
Его каноническое уравнение имеет вид 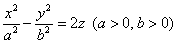 . Данную поверхность также называют седловой поверхностью, а всадники – седлом: . Данную поверхность также называют седловой поверхностью, а всадники – седлом:
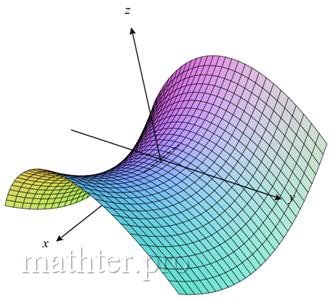
Если его рассекать плоскостями 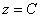 , то в общем случае будут получаться гиперболы , то в общем случае будут получаться гиперболы 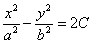 , а при , а при 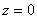 мы получим две пересекающиеся прямые: мы получим две пересекающиеся прямые: 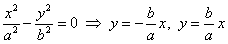 (на чертеже отсутствуют). Таким образом, гиперболический параболоид пересекает плоскость (на чертеже отсутствуют). Таким образом, гиперболический параболоид пересекает плоскость 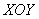 по двум прямым. по двум прямым.
Если его рассекать плоскостями 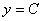 (параллельными плоскости (параллельными плоскости 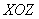 ), то в сечениях будут получаться параболы ), то в сечениях будут получаться параболы 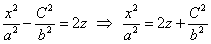 , ветви которых направлены вверх, и множество таких парабол легко увидеть на чертеже. , ветви которых направлены вверх, и множество таких парабол легко увидеть на чертеже.
И, наконец, если параболоид рассекать плоскостями 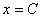 (параллельными плоскости (параллельными плоскости  ), то в сечениях будут получаться параболы ), то в сечениях будут получаться параболы 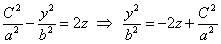 , ветви которых смотрят вниз, эти параболы тоже есть на чертеже. , ветви которых смотрят вниз, эти параболы тоже есть на чертеже.
Таким образом, происхождение гиперболического параболоида полностью расшифровано.
Как и конус, как и «чаша», седло симметрично относительно плоскостей 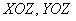 и относительно оси и относительно оси 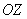 . Рассмотрю один демонстрационный пример: . Рассмотрю один демонстрационный пример:
Задача 181
Построить тело, ограниченное поверхностями 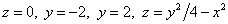 . .
Решение: найдём линии пересечения параболоида с плоскостью 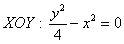 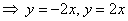 . Слева и справа тело ограничено плоскостями . Слева и справа тело ограничено плоскостями 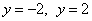 , и ввиду его симметрии достаточно рассмотреть пересечение параболоида с плоскостью , и ввиду его симметрии достаточно рассмотреть пересечение параболоида с плоскостью  : :
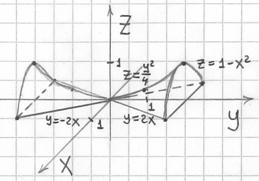 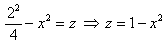 – изобразим эти параболы в плоскостях – изобразим эти параболы в плоскостях  . Осталось «замкнуть» чертёж сверху, для этого найдем пересечение параболоида с фронтальной плоскостью . Осталось «замкнуть» чертёж сверху, для этого найдем пересечение параболоида с фронтальной плоскостью 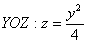 – изобразим эту параболу в плоскости – изобразим эту параболу в плоскости  . Заметьте, что здесь под седлом скрылась ось . Заметьте, что здесь под седлом скрылась ось  , т.к. уравнение неканоническое. , т.к. уравнение неканоническое.
 6.6. Гиперболоиды 6.6. Гиперболоиды
 6.4. Коническая поверхность 6.4. Коническая поверхность
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» Название «эллиптический параболоид» тоже произошло из результатов исследования сечений. В горизонтальных сечениях плоскостями
Название «эллиптический параболоид» тоже произошло из результатов исследования сечений. В горизонтальных сечениях плоскостями 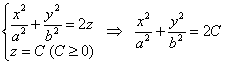 , в частности, при
, в частности, при 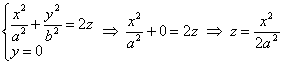 – парабола, лежащая в плоскости
– парабола, лежащая в плоскости 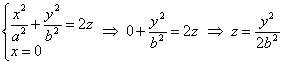 – парабола, лежащая в плоскости
– парабола, лежащая в плоскости 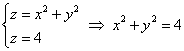 – окружность радиуса 2.
– окружность радиуса 2.

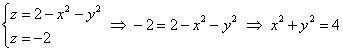 – окружность радиуса 2.
– окружность радиуса 2.

 6.6. Гиперболоиды
6.6. Гиперболоиды 6.4. Коническая поверхность
6.4. Коническая поверхность