|
Ваш репетитор, справочник и друг!
|
4.7. Оценка генеральной долиБыстренько освежим в памяти, что такое доля. Вспоминаем Выборочная доля является точечной оценкой генеральной доли и не внушает особого доверия,
поскольку в разных выборках мы будем получать разные значения Таким образом, наша задача состоит в том, чтобы найти доверительный интервал:
Далее для удобства я буду опускать подстрочный индекс у выборочной доли: Точность оценки Для нахождения Средняя ошибка доли определяется так: В том случае, если генеральная совокупность велика, а выборка малА, то для бесповторной выборки можно использовать и 2-ю
формулу, ибо дробь Пример 29 В целях изучения суточного пробега автомобилей автотранспортного предприятия проведено 10%-ное выборочное обследование 100
автомобилей методом случайного бесповторного отбора, в результате которого получены следующие данные: С вероятностью 0,954 требуется определить долю машин в генеральной совокупности с пробегом более 180 км. Решение: вычислим количество автомобилей с пробегом более 180 км по выборке: Генеральную долю Для уровня доверительной вероятности …Студентам-экономистам почему-то любят предлагать нежные значения «гамма» (у них эта задача – чуть ли не обязательная по
предмету). Причём, в методичках прямо так и пишут без пояснений, что вероятности Вычислим среднюю ошибку доли. Коль скоро выборка 10%-ная, то объём генеральной совокупности равен Таким образом, точность оценки составляет
Ответ: Кстати, тут легко оценить и абсолютное количество таковых машин:
Но результат это, конечно, слабоватый. И помочь здесь может увеличение объёма выборки. Родственная формула уже выведена в
предыдущем параграфе, и я просто заменю дисперсию произведением
И прямо сейчас у вас представится такая возможность. На десерт: Пример 30 Методом механического бесповторного отбора проведено однопроцентное обследование веса пирожных, изготовленных кондитерской
фабрикой за сутки. Распределение веса пирожных по весу следующее: а) С вероятностью 0,9974 определить пределы, в которых будет находиться доля пирожных весом не менее 100 г, во всей суточной продукции б) Сколько процентов пирожных нужно проверить, чтобы увеличить точность оценки в 7 раз? (при той же доверительной вероятности) Оценить целесообразность такого статистического исследования. Краткое решение и ответ в конце книги.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих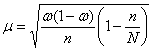 – для
– для 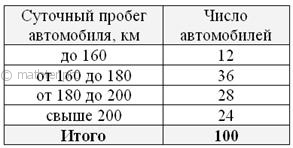
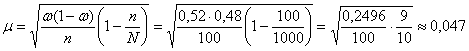
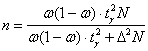 – здесь по желаемой предельной ошибке
– здесь по желаемой предельной ошибке
 4.8. Итоги по главе
4.8. Итоги по главе 4.6. Оценка генеральной средней по повторной и бесповторной выборкам
4.6. Оценка генеральной средней по повторной и бесповторной выборкам