4.6. Оценка генеральной средней по повторной и бесповторной выборкам
Итак, вникаем: пусть из нормально распределенной (или около того) генеральной совокупности
объёма 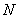 проведена выборка объёма проведена выборка объёма 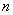 и по её результатам найдена выборочная средняя и по её результатам найдена выборочная средняя 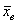 . Тогда доверительный интервал для оценки
генеральной средней . Тогда доверительный интервал для оценки
генеральной средней 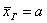 имеет вид: имеет вид:
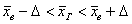 , где , где  («дельта» большая) – точность
оценки, которую также называют предельной ошибкойвыборки. («дельта» большая) – точность
оценки, которую также называют предельной ошибкойвыборки.
Точность оценки рассчитывается как произведение 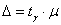 – коэффициента доверия – коэффициента доверия 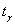 на среднюю ошибкувыборки на среднюю ошибкувыборки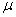 («мю»). («мю»).
Если известна дисперсия генеральной совокупности 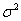 , то коэффициент доверия , то коэффициент доверия 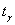 отыскивается из лапласовского соотношения отыскивается из лапласовского соотношения 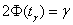 , а средняя ошибка рассчитывается по формуле: , а средняя ошибка рассчитывается по формуле:
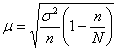 – для бесповторной выборки или – для бесповторной выборки или 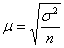 – для повторной. – для повторной.
Если же генеральная дисперсия не известна, то в качестве её приближения используют исправленную выборочную дисперсию 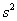 . В этом случае коэффициент доверия . В этом случае коэффициент доверия 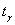 определяют с помощью распределения Стьюдента, а при определяют с помощью распределения Стьюдента, а при 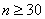 можно использовать соотношение можно использовать соотношение 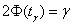 . Средняя же ошибка рассчитывается по аналогичным формулам: . Средняя же ошибка рассчитывается по аналогичным формулам:
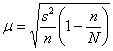 – для бесповторной или – для бесповторной или 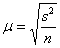 – для повторной выборки. – для повторной выборки.
Напоминаю, что доверительная вероятность (надёжность) 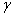 задаётся наперёд и показывает, с какой вероятностью построенный
доверительный интервал задаётся наперёд и показывает, с какой вероятностью построенный
доверительный интервал 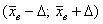 накрывает истинное
значение накрывает истинное
значение 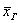 . .
С конспектом отмучились, теперь задачи :)
Модифицируем задание Примера 19, а именно уточним способ отбора попугаев:
Пример 25
Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением 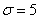 . По результатам 4%-ной бесповторной выборки объёма . По результатам 4%-ной бесповторной выборки объёма 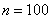 , найдена выборочная средняя , найдена выборочная средняя 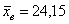 (условно средний рост птицы). (условно средний рост птицы).
1) Найти доверительный интервал для оценки генеральной средней 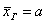 с надежностью с надежностью 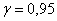 . .
2) Выборку какого объёма нужно организовать, чтобы уменьшить данный интервал в два раза?
Не решение даже, а целое исследование впереди, начинаем. Прежде всего, найдём объём генеральной
совокупности:
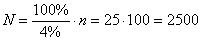 попугаев, и на самом деле нам предстоит
ответить на следующий вопрос: а достаточно ли выборки объёма попугаев, и на самом деле нам предстоит
ответить на следующий вопрос: а достаточно ли выборки объёма 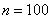 ? Или для качественного исследования роста попугаев нужно выбрать побольше
птиц? ? Или для качественного исследования роста попугаев нужно выбрать побольше
птиц?
1) Доверительный интервал для оценки генеральной средней составим по формуле:
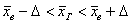 , где , где 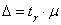 – точность оценки. В задачах данного типа у коэффициента доверия часто
опускают подстрочный индекс и пишут просто – точность оценки. В задачах данного типа у коэффициента доверия часто
опускают подстрочный индекс и пишут просто 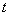 ,
однако я не буду следовать мейнстриму, т. к. эта «кастрация» ухудшает понимание. ,
однако я не буду следовать мейнстриму, т. к. эта «кастрация» ухудшает понимание.
По условию, нам известна генеральная дисперсия, поэтому коэффициент доверия найдём из
соотношения 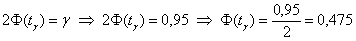 . По таблице значений функции Лапласа либо на макете (пункт 1*) определяем, что этому значению функции соответствует аргумент . По таблице значений функции Лапласа либо на макете (пункт 1*) определяем, что этому значению функции соответствует аргумент 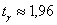 . .
Поскольку выборка бесповторная, то среднюю ошибку рассчитаем по
формуле:
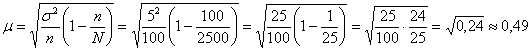
Таким образом, точность оценки 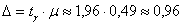 и
соответствующий доверительный интервал: и
соответствующий доверительный интервал:
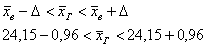
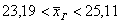 – с вероятностью – с вероятностью 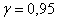 данный интервал накроет истинное значение генерального среднего
роста данный интервал накроет истинное значение генерального среднего
роста 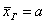 попугая. попугая.
Теперь предположим, что нас не устраивает точность полученного результата. Хотелось бы уменьшить интервал. Или оставить
его таким же, но повысить доверительную вероятность. Этим вопросам и посвящён следующий пункт решения:
2) Выясним, сколько попугаев нужно взять, чтобы уменьшить полученный интервал в два раза. Иными словами, была точность
0,96, а мы хотим  . При условии сохранения
доверительной вероятности необходимый объём выборки можно рассчитать по формуле . При условии сохранения
доверительной вероятности необходимый объём выборки можно рассчитать по формуле 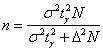 , которая выводится из , которая выводится из 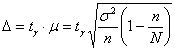 . .
А нашей задаче:
 и обязательно проверочка: и обязательно проверочка:
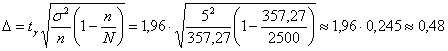 , ч.т.п. , ч.т.п.
Таким образом, чтобы обеспечить точность 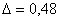 при
надёжности при
надёжности 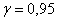 нужно провести выборку объёмом
не менее 358 попугаев (округлили в бОльшую сторону). В этом случае получится доверительный
интервал в два раза короче: нужно провести выборку объёмом
не менее 358 попугаев (округлили в бОльшую сторону). В этом случае получится доверительный
интервал в два раза короче:
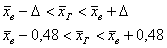
И внимание! Здесь нельзя использовать значение 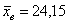 предыдущего пункта! Почему? Потому что в новой выборке мы почти
наверняка получим НОВУЮ выборочную среднюю. Вот её-то и нужно будет подставить. предыдущего пункта! Почему? Потому что в новой выборке мы почти
наверняка получим НОВУЮ выборочную среднюю. Вот её-то и нужно будет подставить.
Осталось прикинуть, а не много ли это – 358 попугаев? Объём выборки составит: 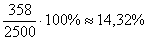 от генеральной совокупности – ну, в принципе, сносно, хотя и многовато. Поэтому здесь
можно использовать другой подход: оставить точность оценки от генеральной совокупности – ну, в принципе, сносно, хотя и многовато. Поэтому здесь
можно использовать другой подход: оставить точность оценки 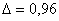 прежней, но повысить доверительную вероятность до прежней, но повысить доверительную вероятность до 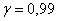 . В этом случае нужно найти новый коэффициент доверия . В этом случае нужно найти новый коэффициент доверия 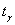 (из соотношения (из соотношения 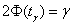 ) и решить уравнение ) и решить уравнение 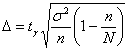 , получив в качестве корня необходимый объём выборки , получив в качестве корня необходимый объём выборки 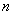 . Желающие могут выполнить этот пункт самостоятельно, в результате
получается выборка в . Желающие могут выполнить этот пункт самостоятельно, в результате
получается выборка в 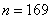 попугаев или попугаев или 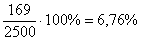 генеральной совокупности. Что лучше, конечно, ведь измерить
линейкой 358 попугаев – задача хлопотная, они явно будут сопротивляться, а некоторые ещё и говорить нехорошие слова J. генеральной совокупности. Что лучше, конечно, ведь измерить
линейкой 358 попугаев – задача хлопотная, они явно будут сопротивляться, а некоторые ещё и говорить нехорошие слова J.
Теперь распишем доверительный интервал 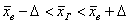 подробно: подробно:
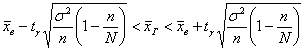
и ответим вот на какой вопрос: а что будет, если генеральная совокупность великА или даже бесконечна? В
этом случае дробь 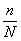 близкА к нулю, и мы получаем
интервал: близкА к нулю, и мы получаем
интервал:
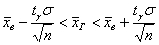 , который фигурировал в Примере 19. То есть по
умолчанию (когда не сказано, бесповторная выборка или нет), считают именно так. , который фигурировал в Примере 19. То есть по
умолчанию (когда не сказано, бесповторная выборка или нет), считают именно так.
Следует отметить, что полученный выше интервал соответствует повторной выборке со
средней ошибкой 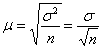 , таким образом, при слишком
большом объёме , таким образом, при слишком
большом объёме 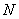 генеральной совокупности
математическое различие между бесповторной и повторной выборкой стирается. генеральной совокупности
математическое различие между бесповторной и повторной выборкой стирается.
Пришло время запланировать собственное статистическое исследование:
Пример 26
В результате многократных независимых измерений некоторой физической величины 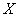 в прошлом достаточно точно определена генеральная дисперсия в прошлом достаточно точно определена генеральная дисперсия 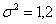 ед.; при этом средняя величина склонна изменениям (от исследования к
исследованию). Сколько измерений нужно осуществить, чтобы с вероятностью ед.; при этом средняя величина склонна изменениям (от исследования к
исследованию). Сколько измерений нужно осуществить, чтобы с вероятностью 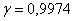 заключить текущее истинное значение генеральной средней заключить текущее истинное значение генеральной средней 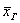 в интервале длиной 0,5 ед. в интервале длиной 0,5 ед.
И это как раз только что описанный случай: данную выборку можно считать бесповторной, при этом ген. совокупность
теоретически бесконечна; либо повторной, так как округлённые результаты измерений могут повторяться.
Краткое решение в конце книги, числа можете выбрать по своему вкусу J. Но здесь есть одно «странное» значение 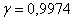 . Оно не случайно и соответствует
правилу «трёх сигм», т. е.,
практически достоверным является тот факт, что построенный интервал накроет истинное значение . Оно не случайно и соответствует
правилу «трёх сигм», т. е.,
практически достоверным является тот факт, что построенный интервал накроет истинное значение 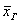 . .
Разумеется, на практике генеральная дисперсия чаще не известна, и поэтому за неимением лучшего, используют исправленную
выборочную дисперсию:
Пример 27
С целью изучения урожайности подсолнечника в колхозах области проведено 5%-ное выборочное обследование 100 га посевов,
отобранных в случайном порядке, в результате которого получены следующие данные:
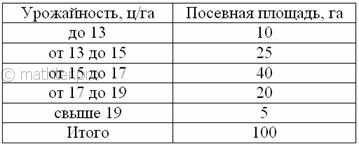
С вероятностью 0,9974 определить предельную ошибку выборки и возможные границы, в которых ожидается средняя
урожайность подсолнечника в области.
Решение: в условии не указан тип отбора, но исходя из логики исследования, положим, что он
бесповторный. Поскольку выборка 5%-ная, то объем генеральной совокупности (общая посевная площадь области)
составляет:
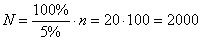 гектаров – не знаю, насколько это
реалистично, оставим этот вопрос на совести автора задачи. гектаров – не знаю, насколько это
реалистично, оставим этот вопрос на совести автора задачи.
По условию, требуется найти предельную ошибку выборки (точность оценки)  , где , где 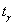 –
коэффициент доверия, соответствующий доверительной вероятности –
коэффициент доверия, соответствующий доверительной вероятности 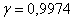 , и коль скоро выборка бесповторна и генеральной дисперсии мы не знаем, то средняя ошибка рассчитывается по формуле , и коль скоро выборка бесповторна и генеральной дисперсии мы не знаем, то средняя ошибка рассчитывается по формуле 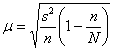 . Далее нужно составить интервал . Далее нужно составить интервал 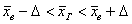 , который с вероятностью 99,74% (практически достоверно) накроет генеральную среднюю , который с вероятностью 99,74% (практически достоверно) накроет генеральную среднюю 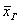 урожайность
подсолнечника по области. урожайность
подсолнечника по области.
И если с коэффициентом «тэ гаммовое» трудностей никаких, то коэффициент «мю» здесь трудовой – по той причине, что нам не
известна исправленная выборочная дисперсия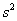 . Ну что же, хороший повод освежить пройденный материал. Смотрим на таблицу
выше и приходим к выводу, что нам предложен интервальный вариационный ряд с
открытыми крайними интервалами. Поскольку длина частичного интервала составляет . Ну что же, хороший повод освежить пройденный материал. Смотрим на таблицу
выше и приходим к выводу, что нам предложен интервальный вариационный ряд с
открытыми крайними интервалами. Поскольку длина частичного интервала составляет 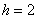 га, то вопрос закрываем так: 11-13 и 19-21 га. га, то вопрос закрываем так: 11-13 и 19-21 га.
Находим середины 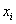 интервалов (переходим к
дискретному ряду), произведения интервалов (переходим к
дискретному ряду), произведения 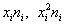 и их суммы: и их суммы:
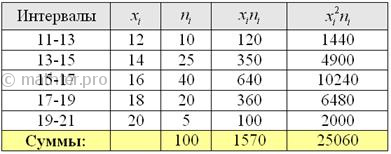
Вычислим выборочную среднюю: 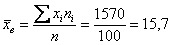 центнеров с гектара. центнеров с гектара.
Выборочную дисперсию вычислим по формуле:
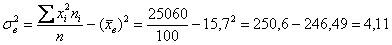 и этим частенько пренебрегают, но я
призываю поправлять дисперсию: и этим частенько пренебрегают, но я
призываю поправлять дисперсию:
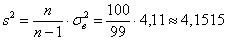 – мелочь, а приятно. – мелочь, а приятно.
Теперь составляем доверительный интервал 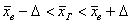 ,
где ,
где 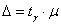 . .
Найдём коэффициент доверия 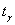 .
Поскольку нам известна лишь исправленная выборочная дисперсия (а не генеральная), то правильнее использовать распределение
Стьюдента. Но, к сожалению, в таблице нет значений для .
Поскольку нам известна лишь исправленная выборочная дисперсия (а не генеральная), то правильнее использовать распределение
Стьюдента. Но, к сожалению, в таблице нет значений для 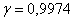 , но зато есть расчётный макет (пункт 2б). Для заданной надёжности и количества степеней свободы , но зато есть расчётный макет (пункт 2б). Для заданной надёжности и количества степеней свободы 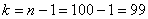 получаем получаем 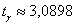 .
Поскольку объём выборки .
Поскольку объём выборки 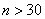 , то можно использовать
нормальное распределение, и тут получается конфетка: , то можно использовать
нормальное распределение, и тут получается конфетка:
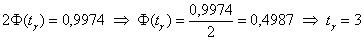 , какой способ выбрать – зависит от вашей
методички, и я так подозреваю, второй :). Но сейчас выберем первый. , какой способ выбрать – зависит от вашей
методички, и я так подозреваю, второй :). Но сейчас выберем первый.
Вычислим среднюю ошибку бесповторной выборки:
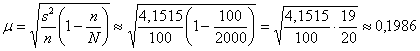 ц/га, таким образом, предельная ошибка
составляет ц/га, таким образом, предельная ошибка
составляет 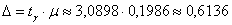 ц/га, и искомый доверительный
интервал: ц/га, и искомый доверительный
интервал:
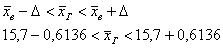
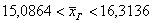 (ц/га) – границы, в которых ожидается
средняя урожайность подсолнечника в области с вероятностью (ц/га) – границы, в которых ожидается
средняя урожайность подсолнечника в области с вероятностью 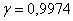 (практически достоверно). (практически достоверно).
Ответ: 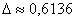 ц/га, ц/га, 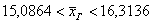 (ц/га) (ц/га)
В рассмотренной задаче можно поставить вопросы, аналогичные Примеру 25, а именно попытаться улучшить исследование, в
частности, уменьшить точность оценки  . В этом
случае для определения необходимого объема выборки используется та же формула . В этом
случае для определения необходимого объема выборки используется та же формула 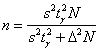 , но она менее достоверна, поскольку в разных выборках мы будем получать разные значения , но она менее достоверна, поскольку в разных выборках мы будем получать разные значения
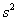 . Такие задачи, однако, встречаются, будьте
готовы. Да, и аналогичная формула для повторной выборки: . Такие задачи, однако, встречаются, будьте
готовы. Да, и аналогичная формула для повторной выборки: 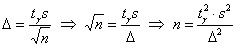 . .
Пример 28
По результатам 10%-ной бесповторной выборки объёма 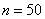 , найдены выборочная средняя , найдены выборочная средняя 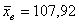 и дисперсия и дисперсия 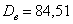 . .
а) Найти пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение генеральной совокупности.
б) Найти эти пределы, если выборка повторная. Какой способ точнее?
Значение 0,954 обусловлено тем, что автор задачи пощадил студентов, в методичке используется функция Лапласа и получается целое значение 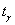 . .
Решаем самостоятельно!
 4.7. Оценка генеральной доли 4.7. Оценка генеральной доли
 4.5. Повторная и бесповторная выборка 4.5. Повторная и бесповторная выборка
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих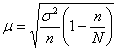 – для
– для 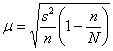 – для бесповторной или
– для бесповторной или 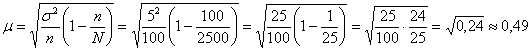
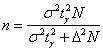 , которая выводится из
, которая выводится из 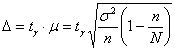 .
.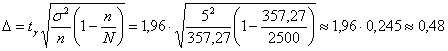 , ч.т.п.
, ч.т.п.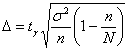 , получив в качестве корня необходимый объём выборки
, получив в качестве корня необходимый объём выборки 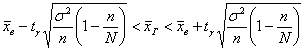

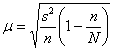 . Далее нужно составить интервал
. Далее нужно составить интервал 
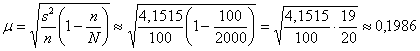 ц/га, таким образом, предельная ошибка
составляет
ц/га, таким образом, предельная ошибка
составляет 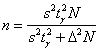 , но она менее достоверна, поскольку в разных выборках мы будем получать разные значения
, но она менее достоверна, поскольку в разных выборках мы будем получать разные значения
 4.7. Оценка генеральной доли
4.7. Оценка генеральной доли 4.5. Повторная и бесповторная выборка
4.5. Повторная и бесповторная выборка