|
Ваш репетитор, справочник и друг!
|
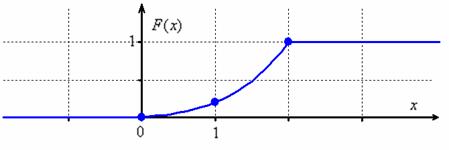
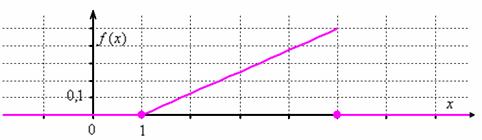
2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?Ответ на этот вопрос состоит из двух слов: с помощью интегралов. Сам смысл математического ожидания и дисперсии мы уже разбирали ранее (но, конечно, повторим), и сейчас настало время узнать, как они определяются для непрерывной случайной величины. Всё очень просто, по аналогии с ДСВ: Математическое ожидание непрерывной случайной величины Как и в дискретном случае, дисперсия не может быть отрицательной! И среднее квадратическое отклонение вычисляется точно так же: Итак, все инструменты в руках и мы с энтузиазмом приступаем к любимому делу: Задача 110 Вычислить Решение начнём как раз с графика функции распределения. При его ручном построении удобно найти промежуточное значение Очевидно, что случайная величина И эти вероятности оцениваются кусками площади, а не значениями функции Ради интереса вычислим: Теперь числовые характеристики. Очевидно, что математическое ожидание (среднеожидаемое значение) случайной величины Убедимся в этом аналитически. По формуле вычисления математического ожидания, и в силу того же свойства аддитивности:
! Примечание: в общем случае (и в этом, в частности) Если промежуток конечен, то можно сразу записывать, что матожидание равно определённому интегралу: Дисперсию (меру рассеяния случайных значений относительно Сначала удобно разделаться с интегралом, здесь я не буду расписывать подробно: Таким образом: И, наконец, среднее квадратическое отклонение: Вот такое вот у нас получилось захватывающее повторение-изучение-исследование! И коль скоро спрашивалось немного, запишем: ответ: Строго говоря, ответ следовало записывать и в предыдущих задачах, но когда пунктов много, то итоговые результаты вполне допустимо помечать по ходу решения, например, подчёркивать или обводить карандашом. Следующее задание для самостоятельного решения: Задача 111 Справка: уравнение прямой, проходящей через точки Однако вся трудность этих заданий состоит в более сложных интегралах, что, собственно, уже не относится к теории вероятностей, и посему я не включил эти примеры в настоящую книгу. Но вот задачка с несобственными интегралами не помешает: Задача 112 Найти Попробуйте решить её самостоятельно! И для желающих есть более трудное задание с функцией Но этим всё дело не ограничивается. Точно так же, как и в дискретном случае, у непрерывной случайной величины существуют особые законы распределения вероятностей, и наиболее популярные из них мы рассмотрим прямо сейчас:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!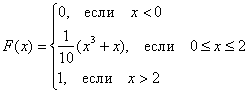
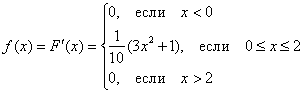
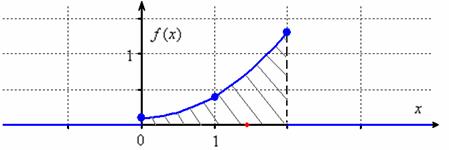
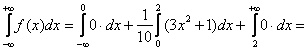
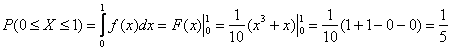 – вероятность того, что случайная величина
– вероятность того, что случайная величина 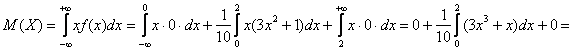
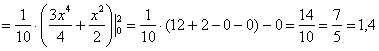 – ну что же, вполне и вполне правдоподобно, результат я отметил красной точкой на чертеже.
– ну что же, вполне и вполне правдоподобно, результат я отметил красной точкой на чертеже.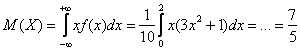
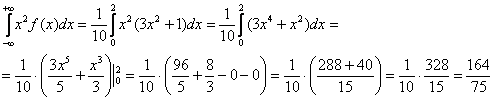
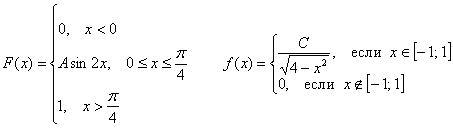
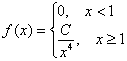
 2.5.1. Равномерное распределение вероятностей
2.5.1. Равномерное распределение вероятностей 2.4.3. Функция ПЛОТНОСТИ распределения вероятностей
2.4.3. Функция ПЛОТНОСТИ распределения вероятностей