|
Ваш репетитор, справочник и друг!
|
2.5.1. Равномерное распределение вероятностейЭто не только «особое», но и, пожалуй, простейшее непрерывное распределение, с помощью которого моделируются многие реальные процессы. И самый такой распространённый пример – это график движения общественного транспорта. Предположим, что некий автобус (троллейбус / трамвай) ходит с интервалом в 10 минут, и вы в случайный момент времени подошли к остановке. Какова вероятность того, что автобус подойдёт в течение 1 минуты? Очевидно, И в самом деле, если длина отрезка (см. чертёж) составляет Суть равномерности состоит в том, что какой бы внутренний промежуток фиксированной длины Рассмотрим типовое задание: Задача 113
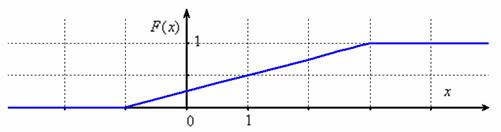
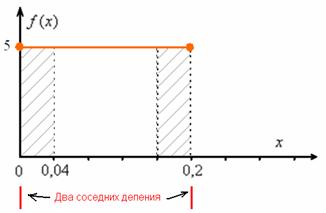
Найти константу Иными словами, всё, о чём только можно было мечтать :) Решение: так как на интервале …почему лучше? Чтобы не было лишних вопросов ;) Таким образом, функция плотности: Выполним чертёж. Значения Найдём математическое ожидание, и, наверное, вы уже догадываетесь, чему оно равно. Вспоминаем «10-минутный» автобус: если случайным образом подходить к остановке много-много дней упаси, то в среднем его придётся ждать 5 минут. Да, именно так – матожидание должно находиться ровно посерединке «событийного» промежутка: Дисперсию вычислим по формуле Таким образом, дисперсия: Составим функцию распределения 1) если 2) если 3) и, наконец, при В результате: Выполним чертёж: Вероятность попадания можно вычислить двумя способами, с помощью найденной функции распределения: И теперь можно записать ответ, перечислив в нём все трофеи, но у меня тут закончилась страница, и поэтому обойдёмся без ответа. За его отсутствие обычно не карают, но иногда заставляют и записать, если рецензенту лень просматривать решения :) Для вычисления Задача 114 Вычислить математическое ожидание и дисперсию. Результаты максимально упростить (формулы сокращённого умножения в помощь). Полученные формулы удобно использовать для проверки, в частности, проверьте предыдущую задачу, подставив в них конкретные значения «а» и «б». И в заключение параграфа разберём парочку «текстовых» задач: Для лучшего понимания решения представим, что это какой-нибудь механический прибор со стрелкой, например, весы с ценой деления 0,2 кг, и нам предстоит взвесить кота в мешке. Но не в целях выяснить его упитанность – сейчас будет важно, ГДЕ между двумя соседними делениями остановится стрелка. Рассмотрим случайную величину Составим функцию плотности распределения вероятностей: 1) Так как расстояние не может быть отрицательным, то на интервале 2) Из условия следует, что стрелка весов с равной вероятностью* может остановиться в любом месте между делениями, включая сами деления, и поэтому на промежутке 3) И поскольку расстояние от БЛИЖАЙШЕГО левого деления не может быть больше, чем 0,2, то при Таким образом: Осталось найти эти площади. Лучше с помощью интегралов, а не по формуле площади прямоугольника. Ибо простота здесь не всегда находит понимание ;) По теореме сложения вероятностей несовместных событий: Легко понять, что максимально возможная погрешность округления составляет 0,1 (100 грамм) и поэтому вероятность того, что ошибка округления не превзойдёт 0,1 равна единице. И из этого, кстати, следует другой, более лёгкий способ решения, в котором нужно рассмотреть случайную величину Ответ: 0,4 И ещё один момент по задаче. В условии речь может идти о погрешностях не округлений, а о случайных погрешностях самих измерений, которые, как правило (но не всегда), распределены по нормальному закону. Таким образом, всего лишь одно слово может в корне изменить решение! Будьте начеку и вникайте в смысл задач! И коль скоро всё идёт по кругу, то ноги нас приносят на ту же остановку: Задача 116 Несмотря на то, что время не может быть отрицательным, интервал
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!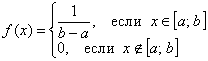
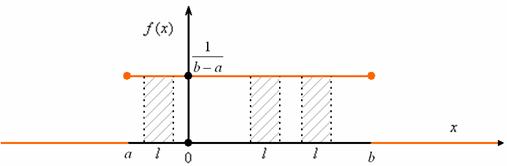
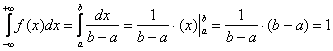 , ч.т.п. С вероятностной точки зрения это означает, что случайная величина
, ч.т.п. С вероятностной точки зрения это означает, что случайная величина 
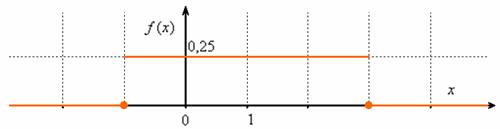
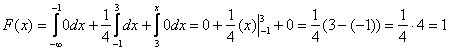
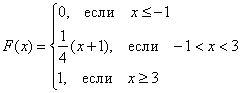
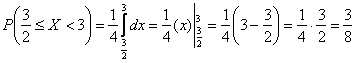
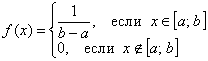 .
.
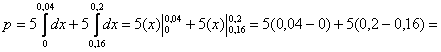
 2.5.2. Показательное распределение вероятностей
2.5.2. Показательное распределение вероятностей 2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?
2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?