|
Ваш репетитор, справочник и друг!
|
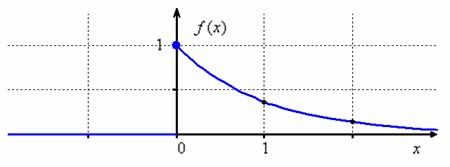
2.5.2. Показательное распределение вероятностейПоказательным или экспоненциальным называют распределение, которое характеризуется следующей функцией плотности:
Убедимся в том, что перед нами не «подделка». Поскольку Используя стандартный алгоритм, легко найти функцию распределения данной случайной величины:
и опять же через общие формулы нетрудно получить числовые характеристики
экспоненциального распределения: Большим достоинством показательного распределения является тот факт, что оно определяется всего лишь одним параметром. Всего лишь
одним, Карл! И по этой причине нам достаточно разобрать одну-единственную задачу, проще всего для Задача 117 Требуется: Одним словом, обычная задача на НСВ, бессмысленная и беспощадная, заметьте, кстати, что в условии ничего не сказано о том, что эта величина распределена по экспоненциальному закону. Решаем: 1) В силу непрерывности функции распределения:
2) Найдём функцию плотности распределения: На всякий случай производная сложной функции: 3) Условие допускает схематическое построение графиков, но зачем занижать планку? Даже при их ручном построении не составляет никакого труда найти пару дополнительных точек и проявить маломальскую аккуратность. Вычислим пару опорных значений: Кстати, о чём идёт речь в 5-м пункте условия? В контексте рассматриваемого примера, нам нужно найти 5) 4) Вычислим математическое ожидание и дисперсию. Несмотря на то, что существуют готовые формулы для расчёта этих характеристик, решать, конечно же, будем подробно. По формуле математического ожидания: Сначала удобно найти неопределенный интеграл: Вспоминаем интегрирование по частям:
Таким образом: Примечание: Дисперсию вычислим по формуле Как и в случае с матожиданием, сначала проясним первообразную: По канонам жанра тут нужно дважды интегрировать по частям, но решение облегчается тем, что после 1-го применения формулы
Таким образом, несобственный интеграл: Примечание: Таким образом: Проверим полученные результаты с помощью готовых формул: Готово. Показательное распределение нашло широкое применение в теории надёжности, этой теме, в частности, посвящены отдельные главы учебного пособия В.Е. Гмурмана. Помимо лампочек и более грустных примеров существуют и другие приложения. Так, например, в простейшем потоке событий время ожидания каждого последующего события распределено именно по экспоненциальному закону. Ну а сейчас пришло время зажечь новые огни и перейти к кульминационному параграфу под названием:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!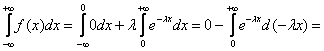
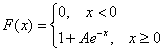
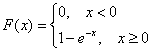 , что
соответствует шаблону
, что
соответствует шаблону 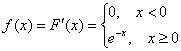 , что
полностью соответствует шаблону.
, что
полностью соответствует шаблону.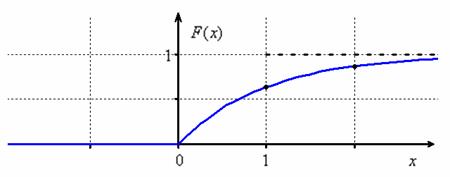
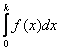 равен вероятности того, что лампочка проработает от 0 до
равен вероятности того, что лампочка проработает от 0 до 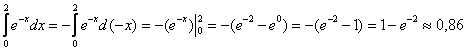 .
.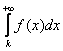 – есть вероятность того, что лампочка проработает более
– есть вероятность того, что лампочка проработает более 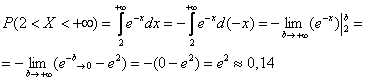
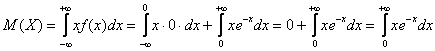
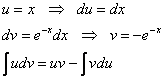
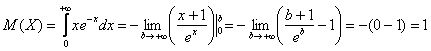
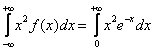
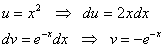
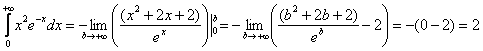
 2.5.3. Нормальное распределение вероятностей
2.5.3. Нормальное распределение вероятностей 2.5.1. Равномерное распределение вероятностей
2.5.1. Равномерное распределение вероятностей