2.3.3. Распределение Пуассона
Случайная величина 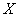 ,
распределённая по этому закону, принимает бесконечное и счётное количество значений ,
распределённая по этому закону, принимает бесконечное и счётное количество значений 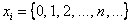 , вероятности появления которых определяются формулой: , вероятности появления которых определяются формулой:
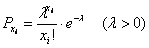
Или, если расписать подробно:

Вспоминая разложение экспоненты в ряд,
легко убедиться, что:
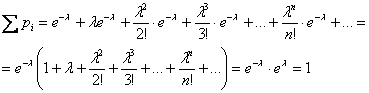
Математическое ожидание пуассоновской случайной величины равно 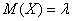 и дисперсия – тому же самому значению: и дисперсия – тому же самому значению: 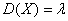 . .
Во всех задачах параграфа Формула Пуассона мы лишь ПОЛЬЗОВАЛИСЬ распределением Пуассона для
приближенного расчёта вероятностей, в то время как ТОЧНЫЕ значения следовало находить по формуле Бернулли, т.е., там имело место биномиальное распределение. И
последующие задачи отличаются принципиально –
– отличие состоит в том, что сейчас речь идёт именно о РАСПРЕДЕЛЕНИИ Пуассона:
Задача 99
Случайная величина 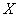 подчинена закону Пуассона с математическим ожиданием,
равным подчинена закону Пуассона с математическим ожиданием,
равным 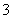 . Найти
вероятность того, что данная случайная величина . Найти
вероятность того, что данная случайная величина 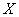 примет значение, меньшее, чем её математическое
ожидание. примет значение, меньшее, чем её математическое
ожидание.
Решение: известно, что математическое ожидание распределения Пуассона в точности равно 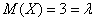 , таким образом, случайная величина , таким образом, случайная величина 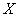 принимает значения принимает значения 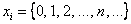 с вероятностями: с вероятностями:
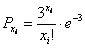
Интересующее нас событие 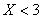 состоит в трёх несовместных исходах: случайная величина состоит в трёх несовместных исходах: случайная величина 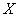 примет значение примет значение 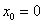 или или 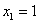 , или , или 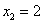 . По теореме сложения вероятностей несовместных событий: . По теореме сложения вероятностей несовместных событий:
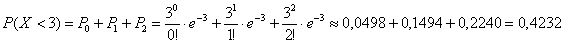 – вероятность
того, что случайная величина – вероятность
того, что случайная величина 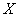 примет значение, меньшее, чем ее математическое
ожидание. примет значение, меньшее, чем ее математическое
ожидание.
Ответ: 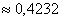
Аналогичная задача на понимание:
Задача 100
Случайная величина 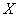 подчинена закону Пуассона с единичным математическим
ожиданием. Найти вероятность того, что данная случайная величина примет положительное значение. подчинена закону Пуассона с единичным математическим
ожиданием. Найти вероятность того, что данная случайная величина примет положительное значение.
Решение и ответ в конце книги.
Помимо прочего, распределение Пуассона нашло широкое применение в теории массового обслуживания для вероятностной характеристики
простейшего потока событий. Постараюсь быть лаконичным:
Пусть в некоторую систему поступают заявки (телефонные звонки, приходящие клиенты и т.д.). Поток заявок называют
простейшим, если он удовлетворяет условиям стационарности, отсутствия последствий и ординарности.
Стационарность подразумевает то, что интенсивность заявок постоянна и не зависит от времени суток, дня недели или других
временнЫх рамок. Иными словами, не бывает «часа пик» и не бывает «мёртвых часов». Отсутствие последствий означает, что
вероятность появления новых заявок не зависит от «предыстории», т.е. нет такого, что «одна бабка рассказала» и другие «набежали» (или
наоборот, разбежались). И, наконец, свойство ординарности характеризуется тем, что за достаточно малый промежуток времени
практически невероятно появление двух или бОльшего количества заявок. «Две старушки в
дверь?» – нет уж, увольте, рубить удобнее по порядку.
Итак, пусть в некоторую систему поступает простейший поток заявок со средней интенсивностью 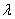 заявок в некоторую единицу времени (минуту,
час, день или в любой другой). Тогда вероятность того, что за данный промежуток времени, в систему поступит ровно заявок в некоторую единицу времени (минуту,
час, день или в любой другой). Тогда вероятность того, что за данный промежуток времени, в систему поступит ровно 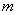 заявок, равна: заявок, равна:
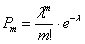
Поразительно, с какой скоростью устаревают задачи:
Задача 101
Звонки в диспетчерскую такси представляет собой простейший пуассоновский поток со средней интенсивностью 30 вызовов в час. Найти
вероятность того, что: а) за 1 мин. поступит 2-3 вызова, б) в течение пяти минут будет хотя бы один звонок.
Решение: используем формулу Пуассона:
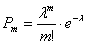
а) Учитывая стационарность потока, вычислим среднее количество вызовов за 1 минуту:
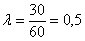 вызова – в среднем
за одну минуту. вызова – в среднем
за одну минуту.
По теореме сложения вероятностей несовместных событий:
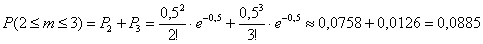 – вероятность
того, что за 1 минуту в диспетчерскую поступит 2-3 вызова. – вероятность
того, что за 1 минуту в диспетчерскую поступит 2-3 вызова.
б) Вычислим среднее количество вызов за пять минут:
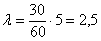
По формуле Пуассона:
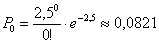 – вероятность
того, что в течение 5 минут не будет ни одного звонка. – вероятность
того, что в течение 5 минут не будет ни одного звонка.
По теореме сложения вероятностей противоположных событий:
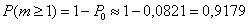 –
вероятность того, что в течение 5 минут будет хотя бы один вызов. –
вероятность того, что в течение 5 минут будет хотя бы один вызов.
Ответ: а) 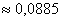 , б) , б) 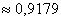
Обращаю внимание, что в отличие от задач параграфа Формула Пуассона, эту задачу уже нельзя
решить по формуле Бернулли. По той причине, что заранее не известно общее количество исходов  (точное количество звонков в тот или иной
час). (точное количество звонков в тот или иной
час).
И предсказать это значение, разумеется, невозможно.
Для самостоятельного решения:
Задача 102
Среднее число автомобилей, проходящих таможенный досмотр в течение часа, равно 3. Найти вероятность того, что: а) за 2 часа пройдут
досмотр от 7 до 10 автомобилей; б) за пол часа успеет пройти досмотр только 1 автомобиль.
Таможня пройдена, достаём припрятанное:
 2.3.4. Гипергеометрическое распределение вероятностей 2.3.4. Гипергеометрическое распределение вероятностей
 2.3.2. Биномиальное распределение вероятностей 2.3.2. Биномиальное распределение вероятностей
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!
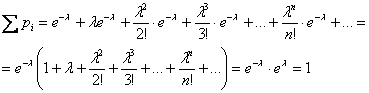
 2.3.4. Гипергеометрическое распределение вероятностей
2.3.4. Гипергеометрическое распределение вероятностей 2.3.2. Биномиальное распределение вероятностей
2.3.2. Биномиальное распределение вероятностей