|
Ваш репетитор, справочник и друг!
|
2.3.2. Биномиальное распределение вероятностейИли биномиальный закон распределения вероятностей. По моим наблюдениям и личной статистике, это наиболее распространённый вид дискретного распределения, с которым мы уже встречались добрый десяток раз. И старая добрая формулировка: Пусть проводится Совершенно понятно, что эта случайная величина может принять одно из следующих значений: Пусть, например: монета подбрасывается 5 раз. Тогда случайная величина или Как вы правильно догадались, соответствующие вероятности определяются формулой Бернулли:
Сведём этот закон распределения в таблицу: Вероятности В нашем примере с монеткой:
Таким образом, закон распределения числа выпавших орлов: Контроль: Легко видеть, что нахождение биномиального ряда – есть занятие муторное, и это хорошо, если он содержит 3-4-5-6 значений. А ведь немало задач, где требуется рассчитать 8-10, а то и бОльшее количество вероятностей! Поэтому вычисления целесообразно автоматизировать в Экселе с помощью его стандартной функции: =БИНОМРАСП(m; n; p; 0), где Именно так реализован Пункт 3 Калькулятора, ну и особо крутая плюшка – это Пункт 6, в котором биномиальное распределение получается автоматически! Однако на практике вычисления нужно расписывать подробно, да и Эксель не всегда бывает под рукой, поэтому держите под рукой
микрокалькулятор и непременно потренируйтесь в ручных вычислениях! Решение: по существу, текст условия совпадает с Задачей 96, но есть одно принципиальное
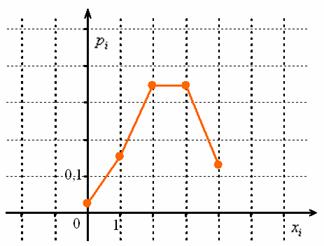
отличие – здесь другая случайная величина. А именно, под страхом расстрела совершается серия из Очевидно, что испытания независимы, попаданий может быть 0, 1, 2, 3 или 4, и посему случайная величина И перед вычислениями удобно сразу «забить» значения 0) 1) 2) 3) 4) Таким образом, искомый закон распределения: Проверка: Пока таблица не ушла из поля зрения, построим многоугольник распределения: Вычислим математическое ожидание и дисперсию. И тут есть отличная новость – для биномиального распределения можно не использовать общий алгоритм расчёта этих числовых характеристик – по той причине, что существуют готовые формулы:
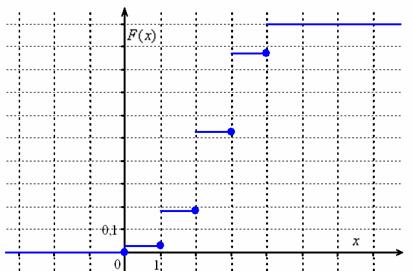
Всегда бы так! Составим функцию распределения вероятностей: Я не буду вновь останавливаться на алгоритме её построения, и если что-то не понятно, то смотрите по ссылке выше. Раз ступенька, два
ступенька – будет график: Найдём Среднее квадратическое отклонение: Готово. Как вариант, в разобранной задаче может быть предложена другая случайная величина: не количество попаданий, а БУДЬТЕ ВНИМАТЕЛЬНЫ! И, конечно же, задачка для самостоятельного решения. Ввиду важности и распространённости биномиального распределения, обязательно прорешайте эту задачу и постукайте пальцами по клавишам микрокалькулятора: Задача 98 Возвращаемся к знакомой фамилии:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!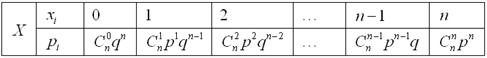


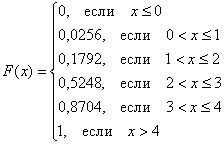
 2.3.3. Распределение Пуассона
2.3.3. Распределение Пуассона 2.3.1. Геометрическое распределение вероятностей
2.3.1. Геометрическое распределение вероятностей