2.3.1. Геометрическое распределение вероятностей
И геометрия тут не при чём.
Пусть проводится серия испытаний, в каждом из которых случайное событие 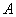 может появиться с вероятностью может появиться с вероятностью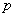 ; причём, испытания заканчиваются при первом же появлении данного события. Тогда случайная величина ; причём, испытания заканчиваются при первом же появлении данного события. Тогда случайная величина 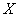 , характеризующая количество совершённых попыток, как раз и имеет геометрическое распределение. , характеризующая количество совершённых попыток, как раз и имеет геометрическое распределение.
Рассмотрим, например, такое событие: 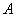 – в результате броска монеты выпадет орёл. – в результате броска монеты выпадет орёл.
Начинаем подбрасывать монету. Совершенно понятно, что вероятность появления орла в любом испытании равна 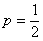 , и наша задача заключается в том, чтобы проанализировать – как скоро появится первый орёл (после чего серия закончится). Составим закон распределения случайной величины , и наша задача заключается в том, чтобы проанализировать – как скоро появится первый орёл (после чего серия закончится). Составим закон распределения случайной величины 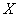 – количества проведённых бросков. – количества проведённых бросков.
Если 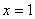 , то это означает, что орёл выпал в первой же попытке. Вероятность этого события равна: , то это означает, что орёл выпал в первой же попытке. Вероятность этого события равна:
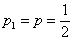
Если 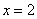 , то в первой попытке выпала решка (вероятность , то в первой попытке выпала решка (вероятность 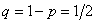 ), а во второй – орёл. По теореме умножения вероятностей ЗАвисимых событий: ), а во второй – орёл. По теореме умножения вероятностей ЗАвисимых событий:
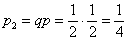
Если 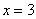 , то в первых двух испытаниях появились решки, а в третьем – орёл. По той же теореме: , то в первых двух испытаниях появились решки, а в третьем – орёл. По той же теореме:
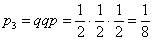
Если 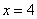 , то первый орёл появился лишь в четвёртом испытании: , то первый орёл появился лишь в четвёртом испытании:
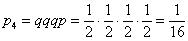
…сколько же можно подбрасывать монету? Теоретически – до бесконечности.
И перед нами пример дискретной случайной величины, которая принимает бесконечное и счётное количество значений. В общем виде её закон распределения записывается следующим образом:

Вероятности 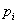 представляют собой бесконечно убывающую геометрическую прогрессию с первым членом представляют собой бесконечно убывающую геометрическую прогрессию с первым членом 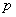 и основанием и основанием 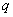 . Отсюда и название – геометрическое распределение вероятностей. Как известно, сумма такой прогрессии равна: . Отсюда и название – геометрическое распределение вероятностей. Как известно, сумма такой прогрессии равна:
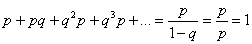 , что полностью соответствует вероятностному смыслу задачи. , что полностью соответствует вероятностному смыслу задачи.
В частности, для примера с «волшебной» монетой:

сумма вероятностей составляет: 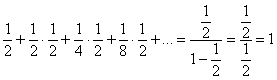
Однако жизнь такова, что всё когда-то заканчивается, и поэтому в практических задачах количество испытаний почти всегда ограничивается. На «грубую» такое распределение тоже можно считать геометрическим, и сейчас мы разберём классический пример:
Задача 96
Стрелок производит несколько выстрелов в цель до первого попадания, имея всего 4 патрона. Вероятность попадания при одном выстреле равна 0,6. Найти закон распределения случайной величины 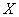 , математическое ожидание , математическое ожидание 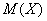 , дисперсию , дисперсию 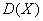 , где , где 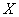 – количество произведённых выстрелов. Построить многоугольник и функцию распределения данной случайной величины. Найти – количество произведённых выстрелов. Построить многоугольник и функцию распределения данной случайной величины. Найти 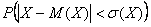 . .
…если что-то позабылось, то я заботливо проставлю ссылки, решаем:
По условию, вероятность попадания в каждом испытании равна 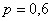 . Тогда вероятность промаха: . Тогда вероятность промаха: 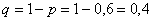 . .
Составим закон распределения случайной величины 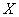 : :
1) 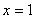
Это означает, что стрелок попал с 1-й попытки и на этом испытания закончились:
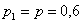
2) 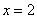 – в первом испытании промах, во втором – попадание. По теореме умножения вероятностей ЗАвисимых событий: – в первом испытании промах, во втором – попадание. По теореме умножения вероятностей ЗАвисимых событий:
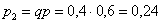
3) 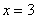 – попадание с третьей попытки, мимо-мимо, попал: – попадание с третьей попытки, мимо-мимо, попал:
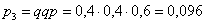
И, наконец:
4) 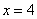
Здесь стрелок может промахнуться или попасть, но испытания заканчиваются в любом случае. Вместе с патронами. По теоремам умножения вероятностей зависимых и сложения вероятностей несовместных событий:
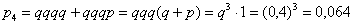
Таким образом, искомый закон распределения:
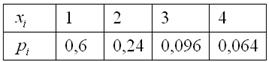
Обязательно выполняем проверку:
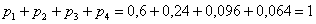 , что и требовалось проверить. , что и требовалось проверить.
Построим многоугольник распределения:
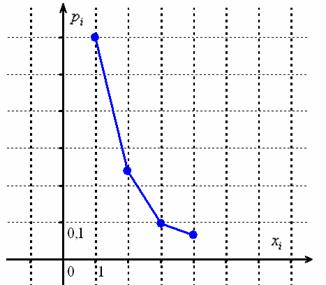
Вычислим 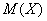 и и 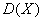 . Для геометрического распределения существуют готовые формулы нахождения математического ожидания и дисперсии: . Для геометрического распределения существуют готовые формулы нахождения математического ожидания и дисперсии: 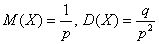 , но нам ими воспользоваться не удастся – по той причине, что количество испытаний не бесконечно. , но нам ими воспользоваться не удастся – по той причине, что количество испытаний не бесконечно.
Поэтому придётся использовать общий алгоритм. Заполним расчётную таблицу:
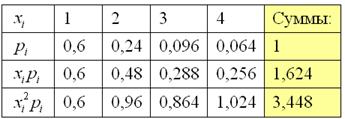
Математическое ожидание лежит готовенькое: 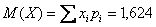 – это среднеожидаемое количество выстрелов (при многократном повторении таких серий из 4 выстрелов). – это среднеожидаемое количество выстрелов (при многократном повторении таких серий из 4 выстрелов).
Дисперсию вычислим по формуле:
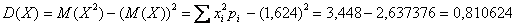 – это мера рассеяния количества выстрелов относительно математического ожидания. – это мера рассеяния количества выстрелов относительно математического ожидания.
Составим функцию распределения вероятностей:

Выполним чертёж:
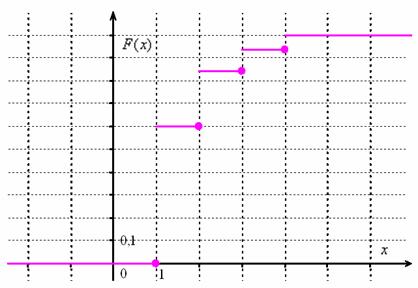
Найдём 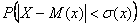 – вероятность того, что значение случайной величины отклонится от математического ожидания не более чем на – вероятность того, что значение случайной величины отклонится от математического ожидания не более чем на 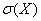 . .
Сначала вычислим среднее квадратическое отклонение:
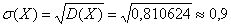
затем – требуемую вероятность:
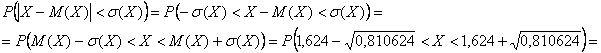 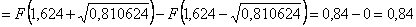 – вспоминаем, что это за интервал, и почему вероятность получилась столь большой ;) – вспоминаем, что это за интервал, и почему вероятность получилась столь большой ;)
Готово!
Но при всей кажущейся простоте, у этого задания существуют подводные камни. Главное коварство состоит в том, условие может быть сформулировано по такому же шаблону, но случайная величина быть ДРУГОЙ. Например:
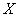 – количество промахов. – количество промахов.
В этом случае закон распределения вероятностей примет следующий вид:

Здесь 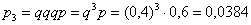 – вероятность того, что будет 3 промаха (и в 4-й попытке попадание); – вероятность того, что будет 3 промаха (и в 4-й попытке попадание); 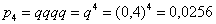 – вероятность того, что стрелок совершит 4 промаха. – вероятность того, что стрелок совершит 4 промаха.
Естественно, что числовые характеристики и содержательные выводы этой задачи будут несколько другими, однако сам закон распределения сохранит свой «геометрический» характер.
Вот ещё одна хитрая вариация, которая мне встречалась на практике:
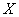 – количество неизрасходованных патронов. – количество неизрасходованных патронов.
Закон распределения этой величины таков:
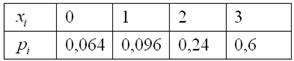
Проанализируйте данный случай самостоятельно. Кстати, в примере, который мы прорешали, случайную величину 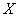 можно эквивалентно сформулировать, как Количество израсходованных патронов. можно эквивалентно сформулировать, как Количество израсходованных патронов.
Таким образом, к решению подобных задач тоже нельзя подходить формально – во избежание ошибок, ВСЕГДА ДУМАЙТЕ ГОЛОВОЙ и анализируйте реалистичность полученных результатов. И тогда полученное значение 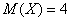 в разобранной задаче вас явно насторожит :) в разобранной задаче вас явно насторожит :)
 2.3.2. Биномиальное распределение вероятностей 2.3.2. Биномиальное распределение вероятностей
 2.2.9. Контрольное задание по ДСВ 2.2.9. Контрольное задание по ДСВ
| Оглавление |
|

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!

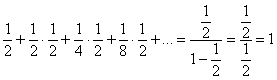





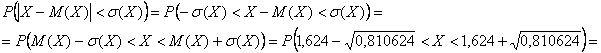


 2.3.2. Биномиальное распределение вероятностей
2.3.2. Биномиальное распределение вероятностей 2.2.9. Контрольное задание по ДСВ
2.2.9. Контрольное задание по ДСВ