|
Ваш репетитор, справочник и друг!
|
2.5.3. Нормальный закон распределения вероятностейБез преувеличения его можно назвать философским законом. Наблюдая за различными объектами и процессами окружающего мира, мы часто
сталкиваемся с тем, что чего-то бывает мало, и что бывает норма. Перед вами принципиальный вид функции плотности нормального распределения вероятностей: Это различные характеристики неодушевленных объектов (те же размеры, вес). Это случайная продолжительность процессов…, снова пришёл на ум грустный пример, и поэтому скажу время «жизни» лампочек :) Из физики вспомнились молекулы воздуха: среди них есть медленные, есть быстрые, но большинство двигаются со «стандартными» скоростями. Более того, даже дискретные распределения бывают близкИ к нормальному, и в конце урока мы раскроем важную предпосылку «нормальности». А сейчас математика, математика, математика, которая в древности не зря считалась философией! Непрерывная случайная величина Эта функция получила фамилию некоронованного короля математики, К.Ф. Гаусса и в своё время была изображена вместе с его портретом
на купюре в 10 немецких марок. Для функции Гаусса выполнены общие свойства плотности, а
именно Следующие замечательные факты я тоже приведу без доказательства:
Эти значения выводятся с помощью общих формул, и желающие могут найти подробные выкладки в учебной литературе. Задача 118 Несмотря на кажущуюся простоту задания, в нём существует немало тонкостей. Первый момент касается обозначений. Они стандартные: матожидание обозначают буквой Решение начнём шаблонной фразой: функция плотности нормально
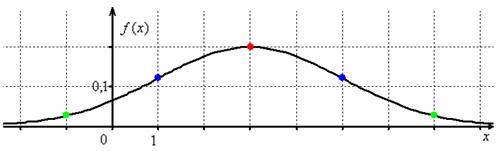
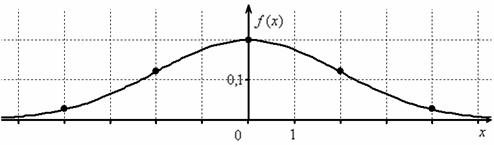
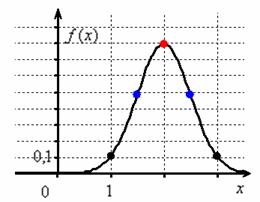
распределённой случайной величины имеет вид Первая, более лёгкая часть задачи выполнена. Теперь график. Вот на нём-то, на моей памяти, студентов «заворачивали» десятки раз, причём, многих неоднократно. По той причине, что график функции Гаусса обладает несколькими принципиальными особенностями, которые нужно обязательно отобразить на чертеже. Сначала полная картина, затем комментарии: по оси абсцисс: 2 тетрадные клетки = 1 ед., И логично, что в первую очередь удобно найти максимум функции: Отмечаем вершину графика (красная точка). Отмечаем синим цветом. Внимание! Далее отклоняемся от центра влево и право ещё на одно стандартное отклонение Отмечаем точки на чертеже (зелёный цвет) и видим, что этого вполне достаточно. На завершающем этапе аккуратно чертим график, и особо аккуратно отражаем его выпуклость / вогнутость! Ну и, наверное, вы давно поняли, что ось абсцисс – это горизонтальная асимптота, и «залезать» за неё категорически нельзя! Поговорим о том, как меняется форма нормальной кривой в зависимости от значений При увеличении или уменьшении «а» (при неизменном «сигма») график сохраняет свою форму и перемещается вправо или
влево соответственно. Так, при В случае изменения «сигмы» (при постоянном «а»), график «остаётся на месте», но меняет форму. При увеличении И как-то незаслуженно осталась в тени функция распределения вероятностей.
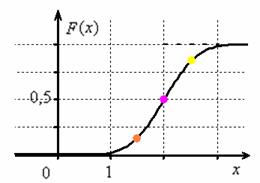
Вспоминаем её определение: Внутри интеграла используют другую букву, чтобы не возникало «накладок» с обозначениями, ибо здесь каждому значению
! Вспоминает также, что: Тут можно снова задействовать Эксель, но есть пара весомых «но»: во-первых, он не всегда под рукой, а во-вторых, «готовые» значения
Об этом я неоднократно рассказывал ранее: в своё время (и ещё не очень давно) роскошью был обычный калькулятор, и в учебной
литературе до сих пор сохранился «ручной» способ решения рассматриваемой задачи. Его суть состоит в том, чтобы свести решение к
стандартному распределению: Зачем это нужно? Дело в том, что значения Итак, вероятность того, что нормальная случайная величина Таким образом, наша задача становится чуть ли не устной! Порой, здесь хмыкают и говорят, что метод устарел. Может быть…, но парадокс состоит в том, что «устаревший метод» очень быстро приводит к результату! И ещё в этом заключена большая мудрость – если вдруг пропадёт электричество или восстанут машины, то у человечества останется возможность заглянуть в бумажные таблицы и спасти мир =) Классика жанра: Задача 119 Решение: в задаче рассматривается нормально распределённая случайная величина Так как речь идёт о перелёте за цель, то Если в вашей методичке дана таблица значений функции Для самопроверки можно «забить» Но гораздо чаще, и в этом курсе в частности, встречается таблица значений функции Лапласа Дробные значения традиционно округляем до 4 знаков после запятой, как это сделано в типовой таблице. И для контроля есть Пункт 5 макета. Напоминаю, что Ответ требуется дать в процентах, поэтому рассчитанную вероятность нужно умножить на 100 и снабдить результат содержательным комментарием: – с перелётом от 5 до 70 м упадёт примерно 15,87% снарядов Тренируемся самостоятельно: Задача 120 В образце решения и далее я буду использовать функцию Лапласа, как самый распространённый вариант. Кстати, обратите внимание, что согласно формулировке, в этой задаче корректнее будет включить концы интервала в рассмотрение. И уже в этом примере нам встретился особый случай – когда интервал
Параметр «дельта» называют отклонением от математического ожидания, и двойное неравенство удобно «упаковать» с помощью модуля:
Таким, образом задача про подшипники решается гораздо короче: Результат этой задачи получился близким к единице, но хотелось бы ещё бОльшей надежности – а именно, узнать границы, в которых находится диаметр почти всех подшипников. Существует ли какой-нибудь критерий на этот счёт? Существует! На этот вопрос отвечает так называемое правило «трех сигм». Его суть состоит в том, что практически достоверным является тот факт, что
нормально распределённая случайная величина Задача 121 Решение очень простое. По условию,
Ответ: Этот пример принципиально отличается от вроде бы похожей задачи параграфа о равномерном распределении. Там была погрешность округления результатов измерений, здесь же речь идёт о случайной погрешности самих измерений. Такие погрешности возникают в связи с техническими характеристиками самого прибора (диапазон допустимых ошибок, как правило, указывают в его паспорте), а также по вине самого экспериментатора – когда мы, например, «на глазок» снимаем показания со стрелки механических весов. Помимо прочих, существуют ещё так называемые систематические ошибки измерения. Это уже неслучайные ошибки, которые возникают по причине некорректной настройки или эксплуатации прибора. Так, например, неотрегулированные напольные весы могут стабильно «прибавлять» килограмм, а продавец систематически обвешивать покупателей. Или не систематически, ведь можно обсчитать :) Однако, в любом случае, случайной такая «ошибка» не будет, и её матожидание отлично от нуля. …срочно разрабатываю курс по подготовке продавцов =) Самостоятельно решаем обратную задачу: Задача 122 Пункт 5* Калькулятора в помощь. Обратите внимание, что здесь не известно математическое ожидание, но это нисколько не мешает решить поставленную задачу. И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала: Задача 123 а) записать плотность вероятности и схематически изобразить ее график; Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в ручном построении чертежа и использовании таблицы ;) После чего мы разберём заключительный пример: Задача 124 Решение: прежде всего, обратим внимание, что в условии ничего не сказано о характере случайной величины. Само по себе присутствие экспоненты ещё ничего не значит: это может оказаться, например, показательное или вообще произвольное непрерывное распределение. И поэтому «нормальность» распределения ещё нужно обосновать: функция Пробуем привести. Для этого выделяем полный квадрат и
организуем трёхэтажную дробь: Таким образом, мы действительно имеем дело с нормальным распределением: Теперь найдём значение параметра Построим график плотности: После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах. Да, и ещё нужно вычислить: Задача была непростой, и посему блеснём академичным стилем, ответ: А теперь обещанный секрет: понятие о центральной предельной теореме. которую также называют теоремой Ляпунова. Её суть состоит в том, что если случайная величина В окружающем мире условие теоремы Ляпунова выполняется очень часто, и поэтому нормальное распределение встречается буквально на каждом шагу. Так, например, молекул воздуха очень и очень много, и каждая из них своим движением оказывает ничтожно малое влияние на всю совокупность. Поэтому скорость молекул воздуха распределена нормально. Большая популяция некоторых особей. Каждая из них (или подавляющее большинство) оказывает несущественное влияние на жизнь всей популяции, следовательно, продолжительность жизни этих особей тоже распределена по нормальному закону. Теперь вернёмся к знакомой задаче, где проводится Именно этот факт мы и использовали в теоремах Лапласа – когда приближали биномиальные вероятности соответствующими значениями функций нормального распределения. Подчёркиваю, что теорема Ляпунова носит статус теоремы, а значит, строго доказана в теории. И в заключение книги хочется ответить на один философский вопрос: имеет ли в нашей жизни значение случайность? Безусловно! Везение играет немаловажную, а порой, и огромную роль: встретить хороших друзей, встретить «своего» человека, найти деятельность по душе и т.д. – всё это нередко происходит благодаря случаю…. Но, с другой стороны, гораздо более важнА системная и упорная деятельность, после которой следуют закономерные результаты. Желательно, полезные, конечно J Дополнительную информацию можно найти в соответствующем разделе портала mathprofi.ru (ссылка на карту раздела). Из учебной литературы рекомендую: Гмурман В. Е. Теория вероятностей и математическая статистика (уч. пособие); Гмурман В. Е. Руководство к решению задач по теории вероятности (задачник с примерами решений).
Везения в главном!
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Практикум по теории вероятностей
Практикум по теории вероятностей Научись решать в считанные дни!
Научись решать в считанные дни!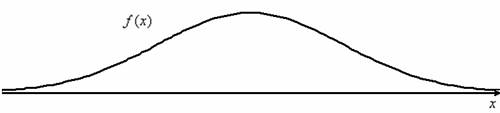
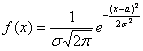 (не пугаемся) и однозначно
определяется параметрами
(не пугаемся) и однозначно
определяется параметрами 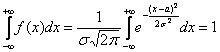 , откуда следует, что нормально
распределённая случайная величина
, откуда следует, что нормально
распределённая случайная величина 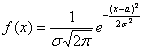 . В данном случае
. В данном случае 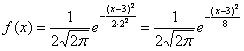
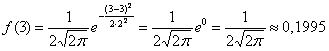


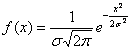 –
чётная, и график симметричен относительно оси ординат.
–
чётная, и график симметричен относительно оси ординат.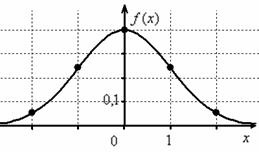
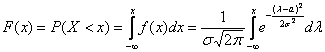 –
вероятность того, что случайная величина
–
вероятность того, что случайная величина 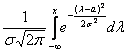 , который равен некоторому числу из интервала
, который равен некоторому числу из интервала
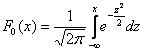 стандартного распределения
стандартного распределения 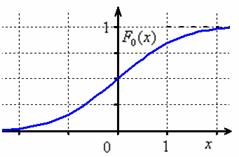
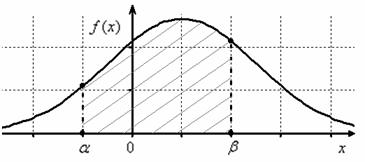
 неразумно, и поэтому здесь рациональнее использовать
«лёгкую» формулу:
неразумно, и поэтому здесь рациональнее использовать
«лёгкую» формулу: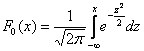
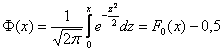 , и с этой
функцией и этой таблицей (см. Приложение Таблицы) мы уже имели дело в
, и с этой
функцией и этой таблицей (см. Приложение Таблицы) мы уже имели дело в 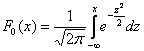 , то используйте формулу
, то используйте формулу 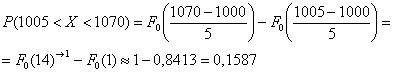
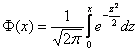 , поэтому решаем через неё:
, поэтому решаем через неё: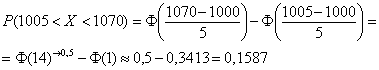
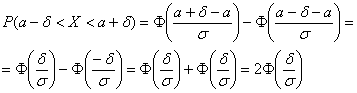
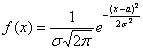 , то случайная величина
, то случайная величина 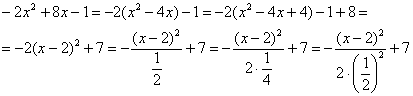
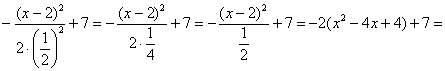
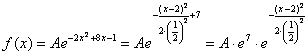 – по
правилу действий со степенями «отщипываем»
– по
правилу действий со степенями «отщипываем» 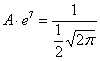 , откуда
выражаем
, откуда
выражаем 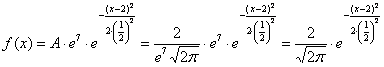 , после чего
ещё раз пробежим глазами и убедимся, что полученная функция имеет вид
, после чего
ещё раз пробежим глазами и убедимся, что полученная функция имеет вид 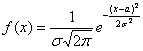 .
.
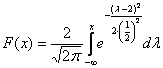 :
:
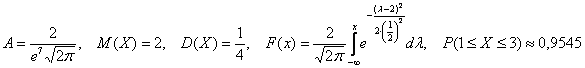
 2.5.2. Показательное распределение вероятностей
2.5.2. Показательное распределение вероятностей