3.6. Неравенства с линиями второго порядка
Они имеют аналогичный смысл, что и неравенства линейные. Такое неравенство определяет некоторую область на плоскости, открытую (без учёта её границы) или замкнутую (с границей).
Так, если уравнение 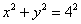 задаёт окружность, то неравенство задаёт окружность, то неравенство 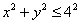 определяет замкнутый круг радиуса определяет замкнутый круг радиуса 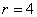 с центром в начале координат. с центром в начале координат.
! Примечание: круг и окружность – не путайте эти понятия!
Координаты любой точки, лежащей внутри круга либо на его границе (на окружности) удовлетворяют данному неравенству. Да хотя бы начало координат 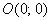 : :
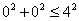
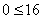 – верное неравенство. – верное неравенство.
Соответственно, неравенству 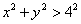 удовлетворяют все точки, лежащие вне этого круга. …Если позабылось, как выглядят линии, то я проставил ссылки. удовлетворяют все точки, лежащие вне этого круга. …Если позабылось, как выглядят линии, то я проставил ссылки.
Аналогично с эллипсом: неравенству 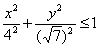 удовлетворяет любая точка, лежащая внутри либо на самом эллипсе. Разумеется, можно рассмотреть и строгое неравенство удовлетворяет любая точка, лежащая внутри либо на самом эллипсе. Разумеется, можно рассмотреть и строгое неравенство 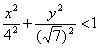 – тогда сам эллипс отпадает. Неравенству – тогда сам эллипс отпадает. Неравенству 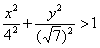 соответствуют все точки, лежащие вне эллипса. соответствуют все точки, лежащие вне эллипса.
Гипербола. Неравенству 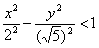 соответствует область, лежащая между ветвей гиперболы. Кстати, как определить нужную область? Точно так же: берём любую точку, которая не принадлежит линии, проще всего взять соответствует область, лежащая между ветвей гиперболы. Кстати, как определить нужную область? Точно так же: берём любую точку, которая не принадлежит линии, проще всего взять 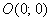 и подставляем её координаты в неравенство: и подставляем её координаты в неравенство: 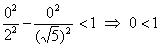 – получено верное неравенство, значит, эта точка и вообще ВСЕ точки этой области удовлетворяют данному неравенству. – получено верное неравенство, значит, эта точка и вообще ВСЕ точки этой области удовлетворяют данному неравенству.
Соответственно, неравенству 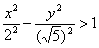 будут удовлетворять ВСЕ точки, которые лежат внутри ветвей гиперболы. Поскольку неравенства строгие, то и там и там сама гипербола не входит в решение. При желании легко выразить левую будут удовлетворять ВСЕ точки, которые лежат внутри ветвей гиперболы. Поскольку неравенства строгие, то и там и там сама гипербола не входит в решение. При желании легко выразить левую 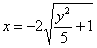 либо правую либо правую 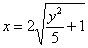 ветвь гиперболы и рассмотреть неравенства, которые определяют ту или иную область (одну из двух) координатной плоскости ветвь гиперболы и рассмотреть неравенства, которые определяют ту или иную область (одну из двух) координатной плоскости  . Ради интереса проведите самостоятельное исследование. . Ради интереса проведите самостоятельное исследование.
И в заключение этого коротенького параграфа:
Устное задание:
Мысленно представьте «школьную» параболу в своём каноническом положении 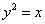 и определите, какие области соответствуют неравенствам и определите, какие области соответствуют неравенствам 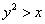 и и 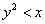 . .
Что для этого нужно сделать, смотрите выше ;)
Продолжаем развивать практическое направление:
 3.7. Задачи с линиями второго порядка 3.7. Задачи с линиями второго порядка
 3.5.2. Поворот и параллельный перенос параболы 3.5.2. Поворот и параллельный перенос параболы
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» 3.7. Задачи с линиями второго порядка
3.7. Задачи с линиями второго порядка 3.5.2. Поворот и параллельный перенос параболы
3.5.2. Поворот и параллельный перенос параболы