|
Ваш репетитор, справочник и друг!
|
3.7. Задачи с линиями второго порядкаСначала вспомним – какие задачи мы уже решали? – на построение линий; И сейчас мы научимся решать ещё одну популярную задачу, которая часто встречается в самостоятельных и контрольных работах: – Найти геометрическое место точек (или составить уравнение множества точек), каждая из которых удовлетворяет определённым аналитическим условиям. Безусловно, данная формулировка является общей и не факт, что в итоге должна получиться обязательно линия, и обязательно второго порядка. Однако в контексте рассматриваемой темы сии магические слова практически всегда вызывают к жизни уравнение окружности, эллипса, гиперболы либо параболы. Кстати, такие задачи вроде есть и в школьной программе, по крайне мере, в факультативном курсе: Задача 103 Составить уравнение линии, расстояние каждой точки которой от точки Решение такой задачи всегда начинается стандартно – в рассмотрение вводится точка Расстояние между двумя точками – это длина соответствующего отрезка, и мы используем элементарную формулу длины отрезка: – расстояние между точками – и между точками Теперь нужно составить уравнение. Согласно условию, расстояние Уравнение успешно составлено, но какую линию оно задаёт – совершенно не понятно. Поэтому дальнейшие действия состоят в упрощении полученной конструкции, и сейчас мы ознакомимся с типовым техническим алгоритмом. Во-первых, избавимся от корней. Для этого возведём в квадрат обе части: Далее, пользуясь формулами Получено уравнение линии 2-го порядка в общем виде. Уже лучше, однако, и оно как неведома зверушка.
А нам нужно определить тип линии. И завершающим штрихом рождаем квадрат в правой части: Аналогичный пример для самостоятельного решения:
Задача 104 Составить уравнение множества точек, для каждой из которых сумма квадратов расстояний от точек Итак, систематизируем порядок решения задачи: На первом шаге необходимо рассмотреть точку На втором шаге следует найти длины нужных отрезков и в соответствии с аналитическим условием задачи составить уравнение. На третьем шаге осуществляем упрощение полученного уравнения. Сначала приводим его к общему виду, а затем к форме, которая близА к канонической. В некоторых задачах получается непосредственно каноническое уравнение. На четвёртом шаге – чертёж и проверка. Чертеж, кстати, требуют далеко не всегда. Кроме того, вас могут попросить продолжить: На пятом шаге – приведение уравнения линии к каноническому виду. На шестом – фокусы, асимптоты, эксцентриситет и т.д. Напоминаю, что находить их гораздо удобнее именно из канонической записи. И мы обязательно продолжим тренироваться: Задача 105 Составить уравнение множества точек, для каждой из которых квадрат расстояния до точки Решение: прежде всего, вчитываемся и разбираемся в условии. Иногда его не удаётся осмыслить с первого раза, но 2-3 попытки
должны помочь :) …Есть? Чему равно расстояние от точки По условию, Таким образом: Раскручиваем гайки: «Икс квадрат» сокращается, и, очевидно, мы имеем дело с уравнением параболы: ! Словесный комментарий должен однозначно определять линию. Теперь вторая часть задачи. Приведём уравнение линии к каноническому виду. И я снова не поленюсь, приведу оба способа: 2) Способ строгий. Перейдём к системе координат Ответ: искомое множество точек представляет собой параболу Если дополнительно нужно найти фокус, директрису и другие характеристики, то пройдите по ссылке – там мы разобрали именно эту параболу. Кстати, по условию не требовалось строить чертежа, но я, конечно, исправил эту недоработку:) Задача 106 Составить уравнение множества точек, для каждой из которых расстояние до точки В образце решения последний пункт реализован обоими способами. Усложняем задание: Задача 107 Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки Решение: пусть точка По условию, для каждой точки Уравнение составлено, но его вид оставляет желать лучшего. Сначала избавимся от трёхэтажной дроби. Для этого знаменатель левой части (дробь)
перекинем направо: Дальнейшие упрощения приобретают знакомые очертания. Возводим обе части в квадрат и раскрываем скобки: Перенесём всё налево и причешем слагаемые: Разделим обе части на 36: Обратите внимание, что такая формулировка однозначно определяет эллипс и добавлять что-то ещё излишне. Изобразим найденный эллипс, точку На практике можно выбрать любую точку эллипса, измерить расстояния линейкой, разделить на калькуляторе В данной задаче уравнение линии нарисовалось сразу в каноническом виде, что облегчает решение. Осталось разобраться с фокусами, эксцентриситетом, асимптотами и директрисами. Очевидно, что у эллипса отсутствуют асимптоты. Вычислим Первый фокус совпал с точкой Найдём эксцентриситет:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»
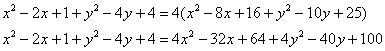
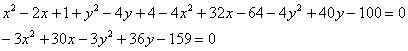
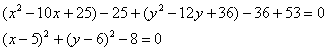
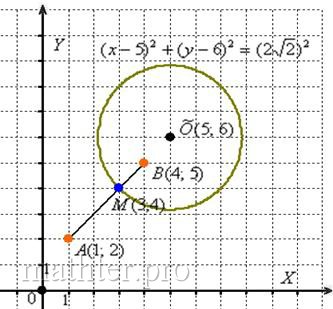 Проведём “любительскую”, но эффективную геометрическую проверку. По условию, для любой точки
Проведём “любительскую”, но эффективную геометрическую проверку. По условию, для любой точки 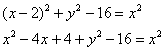
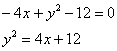
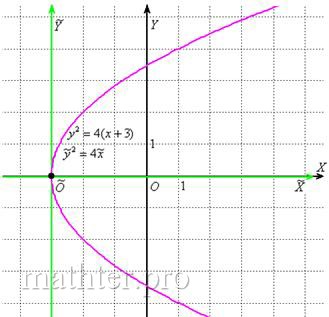 1) Способ «чайниковский». Осуществим
параллельный перенос параболы в начало координат, тогда её уравнение запишется в каноническом виде
1) Способ «чайниковский». Осуществим
параллельный перенос параболы в начало координат, тогда её уравнение запишется в каноническом виде 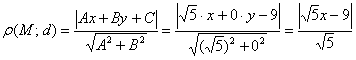 .
.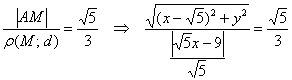
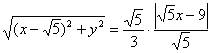
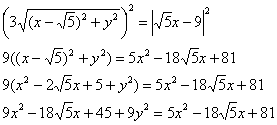
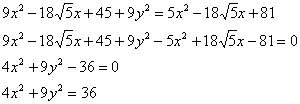
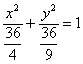 и выполним деление (почему именно так – см. Задачу 99):
и выполним деление (почему именно так – см. Задачу 99):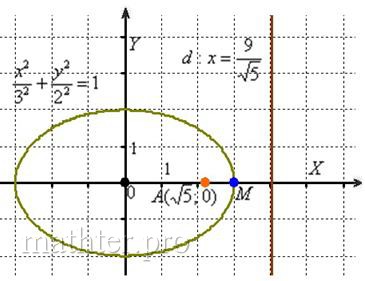 Геометрическая проверка тут затруднена, но с другой стороны
и не сверхъестественна. Возьмём какую-нибудь точку эллипса, проще всего рассмотреть
Геометрическая проверка тут затруднена, но с другой стороны
и не сверхъестественна. Возьмём какую-нибудь точку эллипса, проще всего рассмотреть 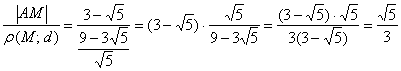 , что и требовалось проверить.
, что и требовалось проверить. 3.7.1. Директрисы эллипса
3.7.1. Директрисы эллипса 3.6. Неравенства с линиями второго порядка
3.6. Неравенства с линиями второго порядка