|
Ваш репетитор, справочник и друг!
|
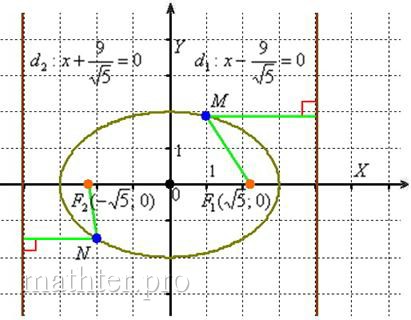
3.7.1. Директрисы эллипсаДа, они есть не только у параболы! – и эта прямая обрела тысячи горячих поклонников J. …Ну что же, шалуны, завидуйте, у эллипса их две! Директрисами эллипса называются две прямые, параллельные малой оси и отстоящие от неё на расстоянии Директрисы лежат вне эллипса и в каноническом положении Так и есть, первая директриса полностью совпала с прямой Эллипс – есть множество всех точек плоскости, таких, что отношение расстояния до каждой точки от фокуса к расстоянию от неё до соответствующей
(ближайшей) директрисы равно эксцентриситету: Со вторым фокусом и директрисой история аналогичная, какую бы точку И не забываем об ответе: искомое геометрическое место точек представляет собой эллипс Похожий пример для самостоятельного решения: Задача 108 Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки Повышаем техническую сложность и знакомимся с новым материалом: Задача 109 Составить уравнение линии, для каждой из которых разность расстояний до точек …здесь уже из условия понятно, о какой кривой идёт речь ;) Решение: пусть точка Корни? Модуль? От модуля избавляемся немедленно: Теперь нужно избавиться от радикалов. Возводить в квадрат сразу – идея плохая (можете попробовать), поэтому разведём корни по углам
ринга: Ну вот, теперь совсем другое дело, возводим обе части в квадрат: Успехи есть, но один корень остался, да ещё и со знаком «+–». Оставим нашего зловреда в одиночестве и максимально упростим левую часть
уравнения: Возводим в квадрат обе части ещё раз, и заметьте, как попутно и совершенно спокойно исчезает знак «+–»: Перебросим всё направо и «развернём» уравнение: Получено уравнение линии 2-го порядка в общем виде. Выделяем полный квадрат при переменной «игрек»,
для этого вынесем «минус девять» за скобку: Далее внутри скобки искусственно добавляем +25 (в целях применения формулы Хорошо осмыслите выполненное действие! – фишка распространённая. Собираем квадрат разности и допиливаем константы: Вот тебе и раз. По всем признакам мыльная опера должна была закончиться гиперболой Изменим знаки у обеих частей: Уже ближе к правде, но «минус» оказался «не на своём месте». Из параграфа о повороте и переносе гиперболы вспоминаем, что это означает поворот данной кривой на 90 градусов относительно своего канонического положения. Но давайте сначала доведём до ума уравнение. Делим обе части на 144: Едем дальше: По условию требуется сначала привести уравнение к каноническому виду, и только потом выполнить чертёж. Дабы не
превысить точку кипения серого вещества, применим упрощенную схему. Однако случай всё равно не самый простой. Центр симметрии нашей подопечной
находится в точке В «чайниковском» способе сначала удобно осуществить параллельный перенос линии Если же сначала повернуть гиперболу вокруг точки Не забывая про асимптоты Ещё раз, где изначально расположена гипербола? В точке Но работать гораздо удобнее с приведённым уравнением. Найдём фокусы: Вычислим эксцентриситет:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»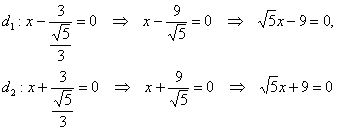
 То есть, для любой точки
То есть, для любой точки 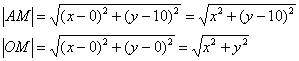
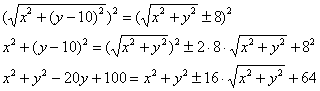
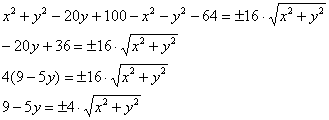
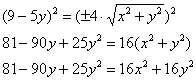
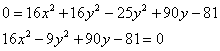
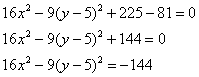
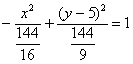

 3.7.2. Директрисы гиперболы
3.7.2. Директрисы гиперболы 3.7. Задачи с линиями второго порядка
3.7. Задачи с линиями второго порядка