6.7.1. Цилиндрическая система координат

По технической сути эта система представляет собой «плоскую» полярную систему координат + дополнительную координату «зет».

В цилиндрической системе координат любая точка пространства однозначно определяется упорядоченной тройкой: полярным радиусом , полярным углом и аппликатой : .

Формулы перехода от декартовой системы к цилиндрической такие же: , а переменная не меняется.

С какими поверхностями удобно иметь дело в цилиндрических координатах? Ну, конечно же, в первую очередь с круглыми цилиндрами.

Так, представим в цилиндрической системе уравнение ( – любое):
, надеюсь, все помнят основное тригонометрическое тождество: .

В чём смысл полученного уравнения? Радиус «эр» ВСЕГДА (при любых «фи» и «зет») равно . А это в точности круглый цилиндр с осью симметрии .

Удачна история и с конусом вращения:
и ,
и с параболоидом вращения:
,
и даже со сферой:
и .

Но для сферы, шара и их частей есть более удобная

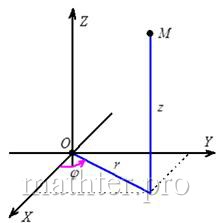
6.7.2. Сферическая система координат

6.6. Гиперболоиды

| Оглавление |

Автор: Aлeксaндр Eмeлин