5.5. Гипотеза о генеральной средней нормального распределения
Постановка задачи такова: предполагается, что генеральная
средняя 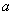 нормального
распределения равна некоторому значению нормального
распределения равна некоторому значению 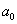 . Это нулевая гипотеза: . Это нулевая гипотеза:
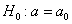
Для проверки гипотезы на уровне значимости 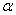 проводится выборка
объема проводится выборка
объема 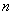 и рассчитывается выборочная средняя и рассчитывается выборочная средняя 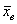 . Исходя из полученного значения и специфики той или иной задачи, можно
сформулировать следующие конкурирующие гипотезы: . Исходя из полученного значения и специфики той или иной задачи, можно
сформулировать следующие конкурирующие гипотезы:
1) 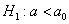
2) 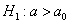
3) 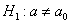
4) 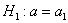 , где , где 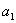 – конкретное альтернативное значение
генеральной средней. – конкретное альтернативное значение
генеральной средней.
При этом возможны две принципиально разные ситуации:
5.5.1. Если генеральная дисперсия 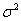 известна известна
Тогда в качестве статистического критерия 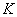 рассматривают случайную величину рассматривают случайную величину 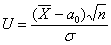 , где , где 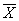 – случайное значение выборочной средней. Почему случайное?
Потому что в разных выборках мы будем получать разные значения – случайное значение выборочной средней. Почему случайное?
Потому что в разных выборках мы будем получать разные значения 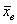 , и заранее предугадать это значение невозможно. , и заранее предугадать это значение невозможно.
Далее находим критическую область. Для конкурирующих гипотез 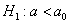 и и 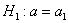 (случай (случай 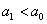 ) строится левосторонняя область, для гипотез ) строится левосторонняя область, для гипотез 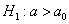 и и 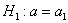 (случай (случай 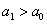 ) – правосторонняя, и для гипотезы ) – правосторонняя, и для гипотезы 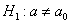 – двусторонняя – по той причине, что
конкурирующее значение генеральной средней может оказаться как больше, так и меньше – двусторонняя – по той причине, что
конкурирующее значение генеральной средней может оказаться как больше, так и меньше 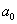 -го. -го.
Чтобы найти критическую область нужно отыскать критическое значение 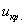 . Оно определяется из соотношения . Оно определяется из соотношения 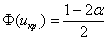 – для односторонней области (лево-
или право-) и – для односторонней области (лево-
или право-) и 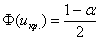 – для
двусторонней области, где – для
двусторонней области, где 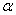 –
выбранный уровень значимости, а –
выбранный уровень значимости, а 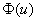 – старая знакомая функция
Лапласа. – старая знакомая функция
Лапласа.
Теперь на основании выборочных данных рассчитываем наблюдаемое значение
критерия:
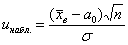
Это можно было сделать и раньше, но такой порядок более последователен и логичен.
Интерпретация результатов зависит от типа критической области:
1) Для левосторонней критической области. Если 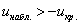 , то гипотеза , то гипотеза 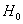 на уровне значимости на уровне значимости 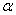 принимается. Если принимается. Если 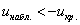 , то отвергается. И картинки тут недавно были, просто заменю букву: , то отвергается. И картинки тут недавно были, просто заменю букву:
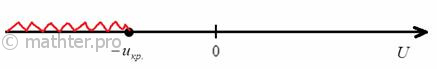
2) Правосторонняя критическая область. Если 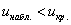 , то гипотеза , то гипотеза 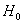 принимается, в случае принимается, в случае 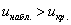 (красный цвет) – отвергается: (красный цвет) – отвергается:
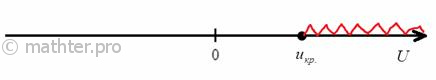
3) Двусторонняя критическая область. Если 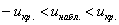 (незаштрихованный интервал), то гипотеза (незаштрихованный интервал), то гипотеза 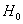 принимается, в противном случае –
отвергается: принимается, в противном случае –
отвергается:
Условие принятия гипотезы здесь часто записывают компактно – с помощью модуля: 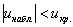
И немедленно приступаем к задачам, а то по студенческим меркам я тут уже на пол диссертации наговорил:)
Пример 31
Из нормальной генеральной совокупности с известной дисперсией 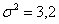 извлечена выборка объёма извлечена выборка объёма 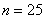 и по ней найдена выборочная средняя и по ней найдена выборочная средняя 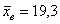 . Требуется на уровне значимости 0,01 проверить нулевую
гипотезу . Требуется на уровне значимости 0,01 проверить нулевую
гипотезу 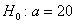 против конкурирующей
гипотезы против конкурирующей
гипотезы 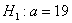 . .
Прежде чем приступить к решению, пару слов о смысле такой задачи. Есть генеральная совокупность с известной
дисперсией и есть веские основания полагать, что генеральная средняя равна 20 (нулевая гипотеза). В результате
выборочной проверки получена выборочная средняя 19,3, и возникает вопрос: это результат случайный или
же генеральная средняя и на самом деле меньше двадцати? – в частности, равна 19 (конкурирующая гипотеза).
Решение: по условию, известна генеральная дисперсия 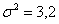 , поэтому для проверки гипотезы , поэтому для проверки гипотезы 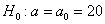 используем случайную величину используем случайную величину 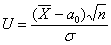 . .
Найдём критическую область. Для этого нужно найти критическое значение. Так как конкурирующее значение
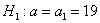 меньше чем меньше чем 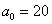 , то критическая область будет
левосторонней (см. теоретический материал выше). , то критическая область будет
левосторонней (см. теоретический материал выше).
Критическое значение определим из соотношения 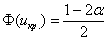 . Для уровня значимости . Для уровня значимости 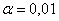 : :
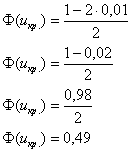
По таблице значений функции Лапласа или с помощью экселевского Макета (пункт 1*) определяем, что этому значению функции соответствует аргумент 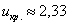 . Таким образом, при . Таким образом, при 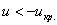 (красная критическая область) нулевая
гипотеза отвергается, а при (красная критическая область) нулевая
гипотеза отвергается, а при 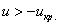 –
принимается: –
принимается:
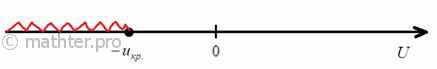
В данном случае 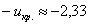 . .
Вычислим наблюдаемое значение критерия:
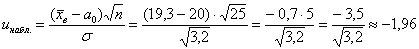
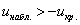 , поэтому на
уровне значимости , поэтому на
уровне значимости 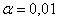 нулевую
гипотезу нулевую
гипотезу 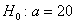 принимаем. принимаем.
Такой, вроде бы неожиданный результат, объясняется тем, что генеральное
стандартное отклонение достаточно великО: 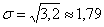 , а посему нет оснований отвергать «главное» значение , а посему нет оснований отвергать «главное» значение 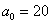 (несмотря на то, что выборочная средняя (несмотря на то, что выборочная средняя 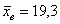 гораздо ближе к конкурирующему
значению гораздо ближе к конкурирующему
значению 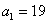 ). Иными словами, такое
значение выборочной средней, вероятнее всего, объясняется естественным разбросом вариант ). Иными словами, такое
значение выборочной средней, вероятнее всего, объясняется естественным разбросом вариант 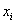 . .
Ответ: на уровне значимости 0,01 нулевую гипотезу принимаем.
Что означает «на уровне значимости 0,01»? Это означает, что мы с 1%-ной вероятностью рисковали отвергнуть
нулевую гипотезу, при условии, что она действительно справедлива. Не забываем, что на самом деле она всё же может быть
и неверной, т.к. существует 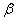 -вероятность того, мы приняли неправильную гипотезу. -вероятность того, мы приняли неправильную гипотезу.
Примеры расчёта мощности критерия 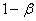 для заданного уровня значимости для заданного уровня значимости 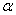 и различных конкурирующих значений можно найти,
например, в учебном пособии и задачнике В. Е. Гмурмана (поздние издания). Это более редкая задача, на которой я не
останавливаюсь в своём курсе, ибо его цель – разобрать наиболее «ходовые» задачи и различных конкурирующих значений можно найти,
например, в учебном пособии и задачнике В. Е. Гмурмана (поздние издания). Это более редкая задача, на которой я не
останавливаюсь в своём курсе, ибо его цель – разобрать наиболее «ходовые» задачи
и, главное – заинтересовать вас математической статистикой!
То была «обезличенная» задача, коих очень много, но мы будем менять мир к лучшему… физическими и химическими способами:)
Заодно и понятнее будет, что здесь к чему:
Пример 32
По результатам 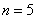 измерений
температуры в печи найдено измерений
температуры в печи найдено 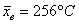 .
Предполагается, что ошибка измерения есть нормальная случайная величина с .
Предполагается, что ошибка измерения есть нормальная случайная величина с 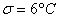 . Проверить на уровне значимости . Проверить на уровне значимости 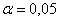 гипотезу гипотезу 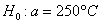 против конкурирующей гипотезы против конкурирующей гипотезы 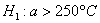 . .
Сначала разберём, в чём жизненность этой ситуации. Есть печка. Для нормального технологического процесса нужна
температура 250 градусов. Для проверки этой нормы 5 раз измерили температуру, получили 256 градусов. Из многократных
предыдущих опытов известно, что среднеквадратическая погрешность измерений составляет 6 градусов (она обусловлена погрешностью
самого термометра и другими случайными обстоятельствами)
И здесь не понятно, почему выборочный результат (256 градусов) получился больше нормы – то ли температура действительно
выше и печь нуждается в регулировке, то ли это просто погрешность измерений, которую можно не принимать во внимание.
Решение: по условию, известно генеральное среднее квадратическое отклонение 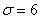 , поэтому для проверки гипотезы , поэтому для проверки гипотезы 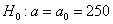 используем случайную величину используем случайную величину 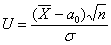 . .
Найдём критическую область. Так как в конкурирующей гипотезе 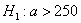 речь идёт о бОльших значениях температуры, то эта область будет
правосторонней. Критическое значение определим из соотношения речь идёт о бОльших значениях температуры, то эта область будет
правосторонней. Критическое значение определим из соотношения 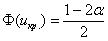 . Для уровня значимости . Для уровня значимости 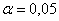 : :
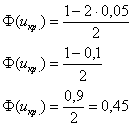
По таблице значений функции Лапласа или с помощью Макета (пункт 1*) определяем, что 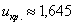 . Таким образом, при . Таким образом, при 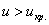 (красный цвет) нулевая гипотеза отвергается, а при (красный цвет) нулевая гипотеза отвергается, а при 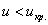 – принимается: – принимается:

Вычислим наблюдаемое значение критерия:
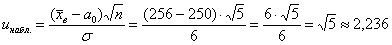
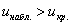 , поэтому на уровне
значимости , поэтому на уровне
значимости 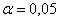 нулевую гипотезу нулевую гипотезу
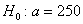 отвергаем. отвергаем.
Как бы сказали статистики, выборочный результат 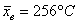 статистически значимо отличается от нормативного значения статистически значимо отличается от нормативного значения 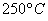 , и печь нуждается в регулировке (для
уменьшения температуры). , и печь нуждается в регулировке (для
уменьшения температуры).
Ответ: на уровне значимости 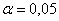 гипотезу гипотезу 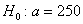 отвергаем. отвергаем.
Ещё раз осмыслим – что означает «на уровне значимости 0,05»? Это означает, что с вероятностью 5% мы отвергли
правильную гипотезу (совершили ошибку 1-го рода). И тут остаётся взвесить риск – насколько критично чуть-чуть уменьшить
температуру (если мы всё-таки ошиблись и температура на самом деле в норме). Если даже небольшое уменьшение температуры
недопустимо, то имеет смысл провести повторное, более качественное исследование: увеличить количество замеров  , использовать более совершенный термометр,
улучшить условия эксперимента и т.д. , использовать более совершенный термометр,
улучшить условия эксперимента и т.д.
Следующая задача для самостоятельного решения, и на всякий случай я ещё раз продублирую ссылку на таблицу значений функции Лапласа и Макет:
Пример 33
Средний вес таблетки сильнодействующего лекарства (номинал) должен быть равен 0,5 мг. Выборочная проверка 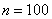 выпущенных таблеток показала, что средний вес
таблетки равен выпущенных таблеток показала, что средний вес
таблетки равен 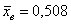 мг. Многократными
предварительными опытами на фармацевтическом заводе установлено, что вес таблеток распределен нормально со средним
квадратическим отклонением мг. Многократными
предварительными опытами на фармацевтическом заводе установлено, что вес таблеток распределен нормально со средним
квадратическим отклонением 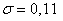 мг. На
уровне значимости мг. На
уровне значимости 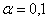 проверить
гипотезу о том, что средний вес таблеток действительно равен проверить
гипотезу о том, что средний вес таблеток действительно равен 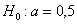 . .
РассмотрИте как конкурирующую гипотезу 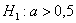 , так и гипотезу , так и гипотезу 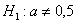 . И в самом деле – ведь полученное значение . И в самом деле – ведь полученное значение 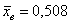 является случайным и в другой выборке оно
может запросто оказаться и меньше чем 0,5. является случайным и в другой выборке оно
может запросто оказаться и меньше чем 0,5.
Краткое решение, как обычно, в конце книги.
Кстати, это ещё один пример, где ошибка 2-го рода (ошибочное принятие неверной нулевой гипотезы), может повлечь
гораздо более тяжелые последствия (опасную передозировку). Поэтому в такой ситуации лучше включить паранойю и увеличить уровень
значимости до 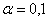 – при этом мы
будем чаще отвергать правильную нулевую гипотезу (совершать ошибку 1-го рода), но зато перестрахуемся и проведём более
тщательное исследование. – при этом мы
будем чаще отвергать правильную нулевую гипотезу (совершать ошибку 1-го рода), но зато перестрахуемся и проведём более
тщательное исследование.
Можно ли одновременно уменьшить вероятности ошибок 1-го и 2-го рода?
(значения 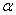 и и 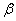 ) )
Да можно. Если увеличить объём выборки. Что совершенно логично.
Теперь вторая ситуация. Та же задача, почти всё то же самое, но:
5.5.2. Генеральная дисперсия НЕ известна
Если значение 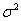 не
известно, то остаётся ориентироваться на исправленную выборочную дисперсию не
известно, то остаётся ориентироваться на исправленную выборочную дисперсию
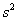 и критерий и критерий 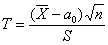 , где , где 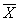 – случайное значение выборочной средней, а – случайное значение выборочной средней, а 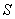 – соответствующее исправленное стандартное отклонение. Данная случайная величина имеет
распределение Стьюдента с – соответствующее исправленное стандартное отклонение. Данная случайная величина имеет
распределение Стьюдента с 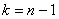 степенями свободы. Алгоритм
решения полностью сохраняется: степенями свободы. Алгоритм
решения полностью сохраняется:
Пример 34
На основании 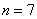 измерений
найдено, что средняя высота сальниковой камеры равна измерений
найдено, что средняя высота сальниковой камеры равна 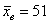 мм и мм и 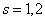 мм. В предположении о нормальном распределении проверить на уровне
значимости мм. В предположении о нормальном распределении проверить на уровне
значимости 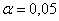 гипотезу гипотезу 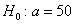 мм против конкурирующей гипотезы мм против конкурирующей гипотезы 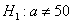 мм. мм.
И начнём мы опять со смысла задачи. Согласно норме, высота сальниковой камеры должна равняться 50 мм. Но по выборке из 7
измерений получено среднее значение 51 мм и за неимением генеральной дисперсии вычислена исправленная
выборочная дисперсия. Возникает вопрос: выборочный результат случаен или нет?
Решение: так как генеральная дисперсия не известна, то для проверки гипотезы 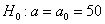 используем случайную величину используем случайную величину 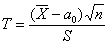 . .
Конкурирующая гипотеза имеет вид 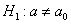 , а значит, речь идёт о двусторонней критической области. Критическое значение можно найти по таблице распределения Стьюдента либо с помощью Макета (пункт 2в). Для уровня значимости , а значит, речь идёт о двусторонней критической области. Критическое значение можно найти по таблице распределения Стьюдента либо с помощью Макета (пункт 2в). Для уровня значимости 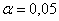 и количества степеней свободы и количества степеней свободы 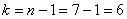 : :
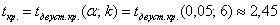
Таким образом, при 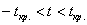 нулевая
гипотеза принимается, и вне этого интервала (в критической области при нулевая
гипотеза принимается, и вне этого интервала (в критической области при 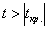 ) – отвергается: ) – отвергается:
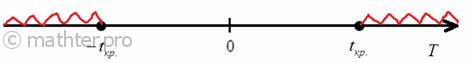
Вычислим наблюдаемое значение критерия:
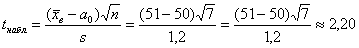 – полученное значение попало в
область принятия гипотезы ( – полученное значение попало в
область принятия гипотезы (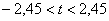 ), поэтому на уровне значимости 0,05 нулевую гипотезу
принимаем. ), поэтому на уровне значимости 0,05 нулевую гипотезу
принимаем.
Ответ: на уровне значимости 0,05 гипотезу 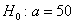 мм принимаем. мм принимаем.
Иными словами, с точки зрения статистики, выборочный результат 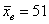 мм, скорее всего (! но это не точно), обусловлен погрешностью
выборки, и на самом деле высота сальниковой камеры соответствует норме (50 мм). мм, скорее всего (! но это не точно), обусловлен погрешностью
выборки, и на самом деле высота сальниковой камеры соответствует норме (50 мм).
Творческая задача для самостоятельного решения:
Пример 35
Нормативный расход автомобильного двигателя составляет 10 л на 100 км. После конструктивных изменений, направленных на
уменьшение этого показателя, были получены следующие результаты 10 тестовых заездов:

На уровне значимости 0,05 выяснить, действительно ли расход топлива стал меньше.
Да, это не редкость – когда нужно не только проверить гипотезу, но и предварительно рассчитать выборочные значения.
Следует отметить, что даже при известной генеральной дисперсии, ориентироваться на неё тут нельзя, ибо
конструктивные изменения могут изменить не только генеральную среднюю, но и генеральную дисперсию.
И в лучших традициях книги, все числа уже забиты в Эксель – там же инструкция по
расчётам выборочных показателей. Если кто-то что-то запамятовал, то вот ролик о
том, как провести эти вычисления быстро (Ютуб).
В данной задаче критическая область левосторонняя, и критическое значение 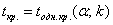 для односторонней области отыскивается по самой нижней строке таблицы или с помощью Макета (тот же пункт 2в). Постарайтесь грамотно оформить решение, образец в конце
книги. Продолжаем. для односторонней области отыскивается по самой нижней строке таблицы или с помощью Макета (тот же пункт 2в). Постарайтесь грамотно оформить решение, образец в конце
книги. Продолжаем.
Как отмечалось в начале главы, статистической является гипотеза либо о
законе распределения статистической совокупности либо о числовых параметрах известных распределений, и начали мы со
второй группы. Таких гипотез воз и маленькая
тележка, и самые популярные из них я только что разобрал. Теперь перейдём к 1-му типу гипотез:
 5.6. Гипотеза о законе распределения генеральной совокупности 5.6. Гипотеза о законе распределения генеральной совокупности
 5.4. Процесс проверки статистической гипотезы 5.4. Процесс проверки статистической гипотезы
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих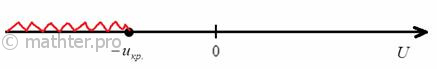
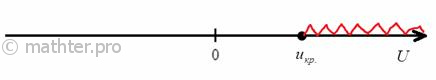
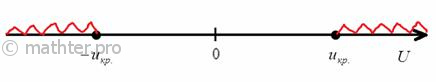
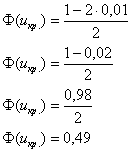
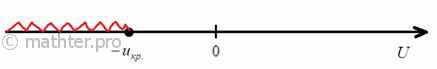
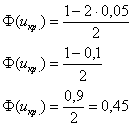

 5.6. Гипотеза о законе распределения генеральной совокупности
5.6. Гипотеза о законе распределения генеральной совокупности 5.4. Процесс проверки статистической гипотезы
5.4. Процесс проверки статистической гипотезы