5.6. Гипотеза о законе распределения генеральной совокупности
Рассмотрим генеральную совокупность, распределение которой неизвестно. Однако
есть основание полагать, что она распределена по некоторому закону 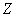 (чаще всего, нормально). Это предположение (об этом
поговорим позже) может появиться как до, так и в результате статистического исследования, когда мы извлекли и изучили выборку объёма (чаще всего, нормально). Это предположение (об этом
поговорим позже) может появиться как до, так и в результате статистического исследования, когда мы извлекли и изучили выборку объёма 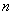 . .
И нам требуется на уровне значимости 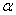 проверить нулевую гипотезу проверить нулевую гипотезу
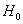 –
о том, что генеральная совокупность распределена по закону –
о том, что генеральная совокупность распределена по закону 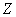 против конкурирующей гипотезы против конкурирующей гипотезы 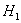 о том, что она по нему НЕ
распределена. о том, что она по нему НЕ
распределена.
Как проверить эту гипотезу?
Постараюсь объяснить кратко. Как мы выяснили ранее, выборочные данные группируются в дискретный или интервальный вариационный
ряд с вариантами 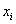 и
соответствующими частотами и
соответствующими частотами 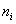 : :
 Так как эти
данные взяты из практического опыта, то выборочный вариационный ряд называют эмпирическим рядом, а частоты Так как эти
данные взяты из практического опыта, то выборочный вариационный ряд называют эмпирическим рядом, а частоты 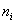 – эмпирическими
частотами. – эмпирическими
частотами.
Далее строятся графики, рассчитываются выборочные характеристики (выборочная
средняя 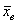 , выборочная дисперсия , выборочная дисперсия 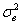 и другие). На основе некоторых выборочных характеристик по
специальным формулам, которые зависят от проверяемого закона и другие). На основе некоторых выборочных характеристик по
специальным формулам, которые зависят от проверяемого закона 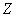 , строится теоретическое распределение, где для тех же
вариант , строится теоретическое распределение, где для тех же
вариант 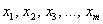 рассчитываются
теоретические частоты рассчитываются
теоретические частоты 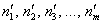 . Эти
частоты моделируют закон . Эти
частоты моделируют закон 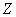 и
наилучшим образом приближают выборочные данные. При этом и
наилучшим образом приближают выборочные данные. При этом 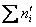 чуть меньше либо равна чуть меньше либо равна 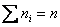 . .
И возникает вопрос: значимо или незначимо различие между эмпирическими 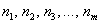 и соответствующими теоретическими и соответствующими теоретическими 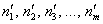 частотами? Для ответа на это вопрос
рассматривают различные статистические критерии, которые называют критериями
согласия, и наиболее популярный из них частотами? Для ответа на это вопрос
рассматривают различные статистические критерии, которые называют критериями
согласия, и наиболее популярный из них
 5.7. Критерий согласия Пирсона 5.7. Критерий согласия Пирсона
 5.5. Гипотеза о генеральной средней нормального распределения 5.5. Гипотеза о генеральной средней нормального распределения
| Оглавление |
|

 Математическая статистика – краткий курс для начинающих
Математическая статистика – краткий курс для начинающих Так как эти
данные взяты из практического опыта, то выборочный вариационный ряд называют эмпирическим рядом, а частоты
Так как эти
данные взяты из практического опыта, то выборочный вариационный ряд называют эмпирическим рядом, а частоты  5.7. Критерий согласия Пирсона
5.7. Критерий согласия Пирсона 5.5. Гипотеза о генеральной средней нормального распределения
5.5. Гипотеза о генеральной средней нормального распределения