Ваш репетитор, справочник и друг!

Математическая статистика – краткий курс для начинающих

5.7. Критерий согласия Пирсона

Спасибо, Карл: …Всем понятно, почему величина случайная? – По той причине, что в разных выборках мы будем получать разные, заранее непредсказуемые эмпирические частоты.

При достаточно большом (объёме выборки) распределение этой случайной величины близкО к распределению хи-квадрат с количеством степеней свободы , где – количество оцениваемых параметров закона .

Далее строится правосторонняя критическая область:

Критическое значение можно найти с помощью соответствующей таблицы или Макета (пункт 3б).

Наблюдаемое значение критерия рассчитывается по эмпирическим и найденным теоретическим частотам:
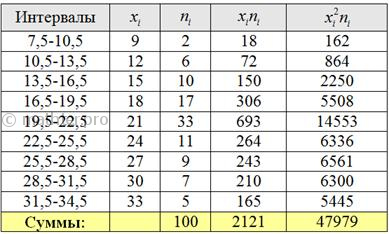
Если , то на уровне значимости нет оснований отвергать гипотезу о том, что генеральная совокупность распределена по закону . То есть, различие между эмпирическими и теоретическими частотами незначимо и, скорее всего, обусловлено случайными факторами (случайностью самой выборки, способом отбора, группировки данных и т.д.)
Если , то нулевую гипотезу отвергаем, иными словами эмпирические и теоретические частоты отличаются значимо, и это различие вряд ли случайно.

И, наконец, коровы, которые нас уже заждались. Реалистичность фактических данных оставлю на совести автора методички сельскохозяйственной академии:

Пример 36

По результатам выборочного исследования найдено распределение средних удоев молока в фермерском хозяйстве (литров) от одной коровы за день:

На уровне значимости 0,05 проверить гипотезу о том, что генеральная совокупность (средний удой коров всей фермы) распределена нормально. Построить эмпирическую гистограмму и теоретическую кривую.

…Если не любите молоко, то пусть это будет чай, сок, пиво или другой напиток, который вам нравится :) Чтобы было интереснее исследовать эту волшебную ферму.

Решение: на уровне значимости проверим гипотезу о нормальном распределении генеральной совокупности против конкурирующей гипотезы о том, что она так НЕ распределена. Используем критерий согласия Пирсона .

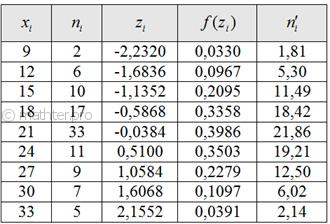
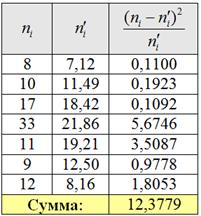
Эмпирические частоты известны из предложенного интервального ряда, и осталось найти теоретические. Для этого нужно вычислить выборочную среднюю и выборочное стандартное отклонение . Выберем в качестве вариант середины частичных интервалов (длина каждого интервала ) и заполним расчётную таблицу:

Вычислим выборочную среднюю: литра.

Выборочную дисперсию вычислим по формуле:

И выборочное стандартное отклонение: литра, по причине большого объёма выборки его исправлением можно пренебречь.
Теоретические частоты рассчитываются по формуле:
, где – функция Гаусса, а .

Входные данные известны: и мы заполняем ещё одну расчётную таблицу:

вычисления удобно проводить в Экселе и на всякий случай я распишу 1-ю строчку:

– здесь выгодно использовать встроенную экселевскую функцию =НОРМРАСП(-2,23; 0; 1; 0), первый аргумент которой равен текущему значению . За неимением Экселя и калькулятора пользуйтесь стандартной таблицей, которая есть в любом учебнике по теорверу.

И, наконец, теоретическая частота: , довольно часто её округляют до целого значения, но без округления результат всё же точнее.

Построим эмпирическую гистограмму с высотой «ступенек» и теоретическую кривую, которая проходит через точки :

Нормальная кривая построена на основе выборочных данных (выборочной средней и стандартного отклонения), и наилучшим образом приближает гистограмму. Дальнейшая задача состоит в том, чтобы оценить, насколько ЗНАЧИМО отличаются эмпирические частоты (ступеньки гистограммы) от соответствующих теоретических частот (уровень коричневых точек).

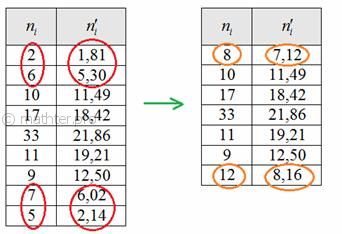
Но перед тем как сравнивать теоретические и эмпирические частоты, следует объединить интервалы с малыми (меньше пяти) частотами. В данном случае объединяем два первых и два последних интервала, для этого суммируем частоты, обведённые красным цветом, и получаем оранжевые результаты:

Это нужно для того, чтобы сгладить неоправданно большое расхождением между малыми частотами по краям выборки. Действие не обязательное, но крайне желательное, ибо студентов на моей памяти из-за этого заставляли переделывать задание.

Найдём критическое значение критерия согласия Пирсона. Количество степеней свободы определяется по формуле , где – количество интервалов, а – количество оцениваемых параметров рассматриваемого закона распределения.

Так как мы объединяли интервалы, то теперь их не девять, а .
У нормального закона мы оцениваем параметра.

Пояснение: – это оценка неизвестного генерального матоожидания, а – это оценка неизвестного генерального стандартного отклонения, итого два оцениваемых параметра.

Таким образом, и для уровня значимости :

Это значение можно найти по таблице критических значений распределения хи-квадрат или с помощью Макета (Пункт 3б).

При нулевая гипотеза отвергается, а при таких оснований нет (заметьте, что формулировка не утверждает истинность гипотезы!):

Вычислим наблюдаемое значение критерия (суть – сумму расхождений между частотами), для этого заполним ещё одну расчётную табличку:

На всякий пожарный пример расчёта: .

В нижней строке таблицы у нас получилось готовое значение , поэтому на уровне значимости 0,05 гипотезу о нормальном распределении генеральной совокупности отвергаем.

Иными словами различие между эмпирическими и теоретическими частотами статистически значимо и вряд ли объяснимо случайными факторами. При этом с вероятностью 5% мы совершили ошибку 1-го рода (то есть, ген. совокупность на самом деле распределена нормально, но мы отвергли верную нулевую гипотезу).

Ответ: на уровне значимости 0,05 гипотезу о нормальном распределении генеральной совокупности отвергаем

В чём может быть причина? Ведь по теореме Ляпунова, большинство коров не оказывают практически никакого влияния на удой других коров, и поэтому распределение ген. совокупности должно быть близкО к нормальному.

Причины могут быть разными. Например, неоднородный состав совокупности (коровы разной породы), или на ферме есть VIP-хлев, где коровы получают улучшенное питание :) А может быть, некоторые коровы больны и как раз оказывают существенное влияние на остальных, в связи с чем нарушается условие теоремы Ляпунова.

Интересно отметить, что при уменьшении уровня значимости до 0,01 критическое значение , и гипотеза о нормальном распределении уже принимается. Однако не нужно забывать, что здесь выросла -вероятность того, что мы приняли неправильную гипотезу (совершили ошибку 2-го рода). С оценкой этой вероятности можно ознакомиться в специализированной литературе по статистике.

И, конечно, в случае сомнений имеет смысл увеличить объём выборки, чтобы провести повторное исследование.

Да, и видео по вычислениям! Хотя особой технической новизны тут нет.

Рассмотренная задача может встретиться в более простой или более сложной формулировке. В версии-«лайт» вам предложат готовые теоретические частоты, где остаётся только проверить гипотезу. Продвинутое же условие звучит примерно так:

На основании исследования выборки выдвинуть гипотезу о законе распределения генеральной совокупности

То есть, здесь не говорится о том, что предполагаемый закон нормальный (или какой-то другой) – этот вопрос вам предлагается проанализировать самостоятельно.

Каким образом это можно сделать?

Во-первых, гипотезу можно выдвинуть априорно, даже не исследуя выборку. В частности, на основании упомянутой выше теоремы Ляпунова: если каждый объект совокупности оказывается ничтожно малое влияние на всю совокупность, то её распределение близкО к нормальному.

Это утверждение носит статус теоремы! То есть, строго доказано в теории.

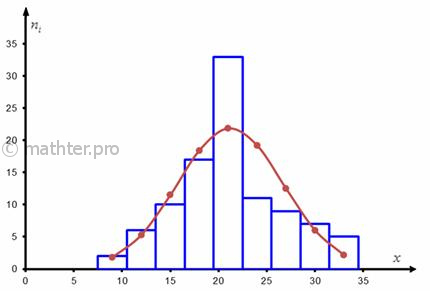
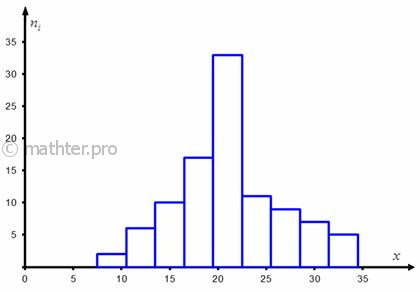
Но по условию, требуют опираться на выборочные данные, и здесь есть сразу несколько признаков, чтобы «вычислить» этот закон. Самый простой и наглядный способ – графический. Грубо говоря, чертим и смотрим. Интервальный вариационный ряд чаще всего изображают гистограммой, возвращаемся к нашим коровам:

Построенная гистограмма по форме напоминает колоколообразный график плотности нормального распределения, и это является веской причиной предположить, что генеральная совокупность распределена нормально. Да, здесь есть слишком высокий средний столбик, но, возможно, это просто случайность выборки.

Если столбики примерно одинаковы по высоте, то предполагаем, что генеральная совокупность распределена равномерно. Для показательного распределениятоже будет своя, характерная гистограмма.

В случае дискретных распределений тоже никаких проблем – строим полигон и смотрим, на что он похож.

Следующие признаки аналитические, приведу их для нормального распределения:

1) У нормального распределения математическое ожидание совпадает с модой и медианой. В нашем случае соответствующие выборочные показатели весьма близкИ друг к другу (матожидание оценивается выборочной средней):

(литры)

Желающие могут рассчитать моду и медиану самостоятельно. Впрочем, желающими часто становятся поневоле, поскольку задача, которую мы рассматриваем, нередко идёт в комплексе со всеми этими заданиями.

2) Выполнение правила «трёх» сигм. Практически все значения нормальной случайной величины находятся в интервале . Найдём этот интервал для нашей выборки. Матожидание «а» оценивается выборочной средней , а стандартное отклонение «сигма» – выборочным стандартным отклонением .Таким образом, наш эмпирический интервал:

– и в него действительно попадают все коровы!

3) Кроме того, есть ещё коэффициенты асимметрии и эксцесса нормального распределения, которые не вошли в этот курс

На практике в исследование желательно включить все пункты за исключением, возможно, третьего (т.к. асимметрию и эксцесс рассчитывают далеко не всегда).

Следует отметить, что перечисленные выше предпосылки ещё не означают, что соответствующая гипотеза будет принята, в чём мы недавно убедились. А если гипотеза и окажется принятой, то это всё равно на 100% не гарантирует нормальность распределения (так как существует -вероятность принять неверную гипотезу (ошибка 2-го рода)).

И, конечно, задача для самостоятельного решения, передаю привет студентам Университета путей сообщения:

Пример 37

В результате проверки 500 контейнеров со стеклянными изделиями установлено, что число повреждённых изделий имеет следующее эмпирическое распределение:

( – количество повреждённых изделий в контейнере, – количество контейнеров) …Здесь тоже представьте изделия по своему интересу :)

С помощью критерия согласия Пирсона на уровне значимости 0,05 проверить гипотезу о том, что случайная величина – число повреждённых изделий распределена по закону Пуассона.

Перелистываем страницу и читаем инструкцию по решению.

Все числа забиты в Эксель, придерживайтесь следующего алгоритма:

1) Находим выборочную среднюю . Это значение будет точечной оценкой параметра «лямбда» теоретического распределения .
2) Находим значения для . Вычисления можно проводить на обычном калькуляторе, но удобнее использовать экселевскую функцию =ПУАССОН(i; «икс выборочное»; 0).

3) Находим теоретические частоты

4) Находим критическое значение критерия согласия Пирсона, где . В данной задаче мы объединяем две последние варианты ввиду их малых частот, следовательно, . Оценивается один параметр («лямбда»), поэтому .

5) Рассчитываем наблюдаемое значение критерия .

6) Делаем вывод.

Примерный образец чистового оформления задачи в конце книги.

5.8. Итоги по главе

5.6. Гипотеза о законе распределения генеральной совокупности

| Оглавление |