5.3.6. Как найти плоскость, перпендикулярную данной?

Очевидно, что к любой плоскости можно провести бесконечно много перпендикулярных плоскостей, и для того, чтобы зафиксировать конкретную перпендикулярную плоскость, нужно задать точку и вектор либо две точки:

Задача 142

Дана плоскость (координаты декартовы). Найти плоскость , перпендикулярную данной и проходящую через точки .

Решение начнём с вопроса задачи: что мы знаем о плоскости ?

Известны две точки. Можно найти вектор , параллельный данной плоскости. Маловато. Было бы неплохо раздобыть ещё один подходящий вектор. Так как плоскости должны быть перпендикулярны, то подойдёт нормальный вектор плоскости (для лучшего понимания задачи отложите вектор нормали от точки в плоскости ).

Проводить подобные рассуждения здОрово помогает схематический чертёж! – повторю этот красный, а точнее, золотой совет :) Итак, задача «раскручена», и решение удобно оформить по пунктам (это совет серебряный:):

1) Найдём вектор .

2) Из уравнения снимем вектор нормали: .

3) Уравнение плоскости составим по точке (можно взять ) и двум неколлинеарным векторам :

Ответ:

Проверка состоит из двух этапов:

1) Проверяем, действительно ли плоскости будут перпендикулярны. Если две плоскости перпендикулярны, то их векторы нормали будут ортогональны. Логично. Из полученного уравнения снимаем вектор нормали и рассчитываем скалярное произведение векторов:
, а значит,

К слову, здесь мы разобрали ещё одну задачу – проверили плоскости на перпендикулярность, и теперь вы знаете, как это сделать.

2) В уравнение плоскости подставляем координаты точек . Обе точки должны «подойти».

И первый, и второй пункт можно выполнить устно. Но выполнить обязательно! И это уже даже не платиновый совет – это аксиома!

…Что-то не хочется мне вас сегодня отпускать…, наверное, хорошо себя вели и добросовестно прорешали все задачи =) Придётся рассказать что-нибудь ещё:

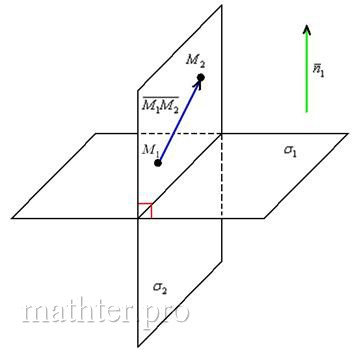
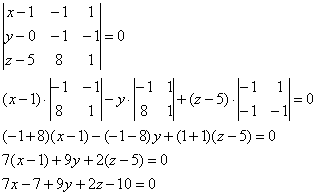
5.3.7. Взаимное расположение трёх плоскостей

5.3.5. Как найти угол между плоскостями?

| Оглавление |

Автор: Aлeксaндр Eмeлин