6.5.1. Как найти собственные значения и собственные векторы?
Только что я выставил собственный вектор «главным действующим лицом», но на самом деле это не совсем так: сначала разыскиваются собственные значения и только потом соответствующие им собственные векторы. Часто ещё говорят, что собственный вектор 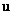 соответствует собственному значению соответствует собственному значению 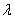 . .
Проведём небольшое исследование и получим алгоритм, по которому нужно решать эту задачу:
Пример 137
Найти собственные числа и собственные векторы линейного оператора, заданного матрицей 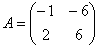 – это матрица, для которой я уже «выдал» одно собственное значение и один собственный вектор. Давайте научимся добывать их самостоятельно! – это матрица, для которой я уже «выдал» одно собственное значение и один собственный вектор. Давайте научимся добывать их самостоятельно!
Решение: обозначим через 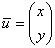 неизвестный собственный вектор и примЕним к нему предложенный оператор. Тогда соответствующее матричное уравнение неизвестный собственный вектор и примЕним к нему предложенный оператор. Тогда соответствующее матричное уравнение 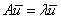 запишется следующим образом: запишется следующим образом:
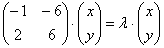
В левой части по обычному правилу проведём матричное умножение, в правой части – внесём «лямбду»:
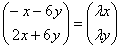
Две матрицы равны, если равны их соответствующие элементы. Таким образом, получаем однородную систему линейных уравнений:
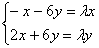 – перенесём всё налево: – перенесём всё налево: 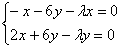 – после чего в первом уравнении вынесем за скобки «икс», а во втором – «игрек»: – после чего в первом уравнении вынесем за скобки «икс», а во втором – «игрек»:
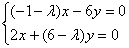
По определению, собственный вектор не может быть нулевым 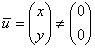 , поэтому нас не устраивает тривиальное решение , поэтому нас не устраивает тривиальное решение 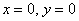 системы. Следовательно, уравнения линейно зависимы и определитель матрицы системы равен нулю: системы. Следовательно, уравнения линейно зависимы и определитель матрицы системы равен нулю:
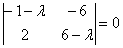
Перед вами так называемое характеристическое уравнение линейного оператора. Корни этого уравнения – и есть собственные числа данного преобразования.
Сначала найдём собственные числа. Раскроем определитель и решим квадратное уравнение (см. Приложение Горячие школьные формулы):
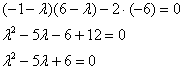
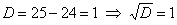 , таким образом, собственные значения: , таким образом, собственные значения:
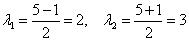 – их желательно нумеровать и располагать в порядке возрастания (хотя, это не принципиально). – их желательно нумеровать и располагать в порядке возрастания (хотя, это не принципиально).
Теперь найдём собственные векторы. В данном примере получены различные собственные числа и каждому из них соответствует свой собственный вектор:
1) Рассмотрим собственное число 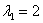 и подставим значение и подставим значение 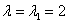 в однородную систему уравнений в однородную систему уравнений 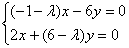 : :
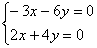
Для записи системы удобно использовать формальный приём: мысленно либо на черновике подставляем 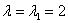 в определитель в определитель 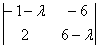 : :
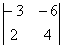 – это и есть коэффициенты системы. – это и есть коэффициенты системы.
Из обоих уравнений следует:
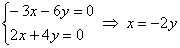
Если в ходе решения выяснилось, что линейной зависимости нет (т. е. получается только тривиальное решение 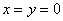 ) – ищите ошибку! Этот признак касается всех задач рассматриваемого типа. ) – ищите ошибку! Этот признак касается всех задач рассматриваемого типа.
Итак, в нашем распоряжении есть выражение 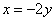 , и, придавая переменной «игрек» (либо «икс») произвольные значения, мы получаем, вообще говоря, бесконечно много собственных векторов , и, придавая переменной «игрек» (либо «икс») произвольные значения, мы получаем, вообще говоря, бесконечно много собственных векторов 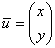 . Но все они коллинеарны друг другу, и поэтому достаточно указать одного «представителя». Обычно стараются выбрать «красивый» вектор – чтобы его «иксовая» координата была положительной, целой и минимальной. . Но все они коллинеарны друг другу, и поэтому достаточно указать одного «представителя». Обычно стараются выбрать «красивый» вектор – чтобы его «иксовая» координата была положительной, целой и минимальной.
Этому эстетическому критерию соответствует значение 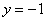 , тогда: , тогда:
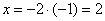
Теперь обязательно проверяем, что частное решение 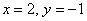 удовлетворяет каждому уравнению системы: удовлетворяет каждому уравнению системы:
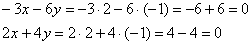
Таким образом: 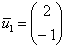 – первый собственный вектор. – первый собственный вектор.
2) Найдём собственный вектор, соответствующий числу 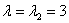 . Для этого подставим его в определитель . Для этого подставим его в определитель 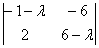 и запишем вторую однородную систему: и запишем вторую однородную систему:
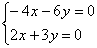
Из обоих уравнений системы следует, что 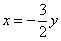 . Придавая «игреку» или «иксу» произвольные значения, мы опять получим бесконечное множество коллинеарных друг другу векторов. Выберем «стильный» экземпляр – с положительной, целой и наименьшей иксовой координатой. Этому пожеланию соответствует значение . Придавая «игреку» или «иксу» произвольные значения, мы опять получим бесконечное множество коллинеарных друг другу векторов. Выберем «стильный» экземпляр – с положительной, целой и наименьшей иксовой координатой. Этому пожеланию соответствует значение 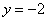 , тогда: , тогда:
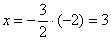 – и для проверки мысленно подставляем комплект – и для проверки мысленно подставляем комплект 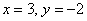 в каждое уравнение системы (см. выше). в каждое уравнение системы (см. выше).
В результате: 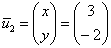 – второй собственный вектор. – второй собственный вектор.
Ответ: собственные числа: 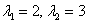 , соответствующие собственные векторы: , соответствующие собственные векторы:
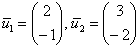 . .
Промежуточных «контрольных точек» было достаточно, но генеральная проверка не помешает: 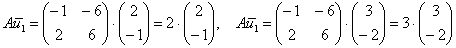 . .
В чём смысл этой задачи?
Оператор, заданный матрицей 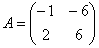 (в некотором базисе), определённым образом преобразует все векторы некоторого двумерного линейного пространства. Но хотелось бы прояснить типичные особенности этого преобразования. Что и позволяют сделать найденные трофеи. А именно, данный оператор сохраняет направления векторов (в некотором базисе), определённым образом преобразует все векторы некоторого двумерного линейного пространства. Но хотелось бы прояснить типичные особенности этого преобразования. Что и позволяют сделать найденные трофеи. А именно, данный оператор сохраняет направления векторов 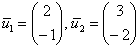 и иже с ними коллинеарных векторов. Заметим, что сами векторы и иже с ними коллинеарных векторов. Заметим, что сами векторы 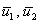 неколлинеарны, таким образом, имеем два множества векторов – два направления, которые этот оператор сохраняет. При этом он «вытягивает» все векторы первой группы в неколлинеарны, таким образом, имеем два множества векторов – два направления, которые этот оператор сохраняет. При этом он «вытягивает» все векторы первой группы в 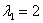 раза, а все векторы второй группы – в раза, а все векторы второй группы – в 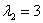 раза. раза.
И ещё один момент касается обозначений: координаты собственных векторов довольно часто записывают не в столбцы, а в строки, например: 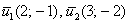 (и, если честно, я сам привык записывать их строками). Такой вариант приемлем, но в свете темы линейных преобразований технически удобнее использовать вектор-столбцы. (и, если честно, я сам привык записывать их строками). Такой вариант приемлем, но в свете темы линейных преобразований технически удобнее использовать вектор-столбцы.
Тренируемся самостоятельно:
Пример 138
Найти собственные числа и собственные векторы матрицы 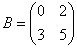
В типовой задаче, конечно, не нужно проводить целое «исследование» по образцу предыдущего примера, сразу записываем характеристический определитель – и вперёд. Примерный образец чистового оформления решения в конце книги.
 6.5.2. Линейное преобразование в базисе из собственных векторов 6.5.2. Линейное преобразование в базисе из собственных векторов
 6.5. Собственные числа и собственные векторы линейного преобразования 6.5. Собственные числа и собственные векторы линейного преобразования
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих
 6.5.2. Линейное преобразование в базисе из собственных векторов
6.5.2. Линейное преобразование в базисе из собственных векторов 6.5. Собственные числа и собственные векторы линейного преобразования
6.5. Собственные числа и собственные векторы линейного преобразования