6.5.2. Линейное преобразование в базисе из собственных векторов
Вернёмся к подопытному линейному преобразованию Примера 137. Оно записано в матричной форме 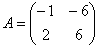 , а значит, задано в некотором базисе двумерного векторого пространства. Однако базисов в нём не счесть и мы можем перейти к произвольному базису, в результате чего получится другая (в общем случае) матрица , а значит, задано в некотором базисе двумерного векторого пространства. Однако базисов в нём не счесть и мы можем перейти к произвольному базису, в результате чего получится другая (в общем случае) матрица  того же самого преобразования в новом базисе. того же самого преобразования в новом базисе.
Но базис базису рознь и есть особо удобные базисы….
Если линейный оператор  n-мерного векторого пространства задан матрицей n-мерного векторого пространства задан матрицей  в некотором базисе и имеет в некотором базисе и имеет 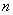 линейно независимых собственных векторов (что бывает не всегда), то матрицу оператора можно представить в виде: линейно независимых собственных векторов (что бывает не всегда), то матрицу оператора можно представить в виде:
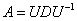 , где , где 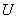 – матрица перехода к базису из собственных векторов, а – матрица перехода к базису из собственных векторов, а 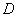 – матрица того же линейного преобразования в базисе из собственных векторов. И «дэ» – это есть в точности диагональная матрица с соответствующими собственными числами. – матрица того же линейного преобразования в базисе из собственных векторов. И «дэ» – это есть в точности диагональная матрица с соответствующими собственными числами.
В нашем двумерном примере собственные векторы 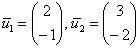 линейно независимы (неколлинеарны), а значит, образуют базис. Запишем матрицу перехода к этому базису: линейно независимы (неколлинеарны), а значит, образуют базис. Запишем матрицу перехода к этому базису: 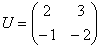 – напоминаю, что координаты нужно записывать в столбцы и строго по порядку – сначала первый вектор базиса, затем второй. – напоминаю, что координаты нужно записывать в столбцы и строго по порядку – сначала первый вектор базиса, затем второй.
На главной диагонали матрицы 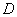 в соответствующем порядке располагаются собственные числа в соответствующем порядке располагаются собственные числа 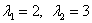 , а остальные элементы равняются нулю: , а остальные элементы равняются нулю:
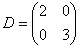
! И снова о важности порядка: перестановка «двойки» и «тройки» недопустима!
По стандартному алгоритму находим обратную матрицу 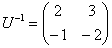 . …Нет, это не опечатка – перед вами редкое, как солнечное затмение событие, когда обратная совпала с исходной матрицей. . …Нет, это не опечатка – перед вами редкое, как солнечное затмение событие, когда обратная совпала с исходной матрицей.
Осталось записать линейное преобразование в виде 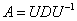 : :
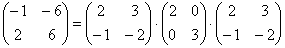 , где , где 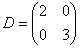 – матрица данного линейного преобразования в базисе из собственных векторов. Она проще, нежели – матрица данного линейного преобразования в базисе из собственных векторов. Она проще, нежели 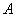 . .
Иногда представление 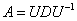 называют каноническим или спектральным разложением матрицы называют каноническим или спектральным разложением матрицы 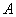 . .
Поскольку матрицы 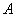 и и 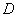 подобны, то они обладают знакомыми инвариантами. А именно, равны их определители: подобны, то они обладают знакомыми инвариантами. А именно, равны их определители: 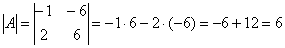 , сразу оценИте удобство базиса: , сразу оценИте удобство базиса: 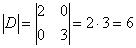 . И равны следы: . И равны следы: 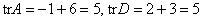 . .
Но это далеко не всё! Важнейший инвариант подобных матриц – это собственные числа, а значит, и их «родственник» – характеристический многочлен. В самом деле, составим характеристическое уравнение матрицы 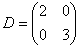 : :
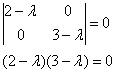
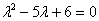 – в результате получен тот же самый многочлен – в результате получен тот же самый многочлен 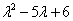 с корнями с корнями 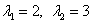 , что и для матрицы , что и для матрицы 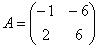 в Примере 137. в Примере 137.
Таким образом, линейное преобразование во всех возможных базисах имеет матрицы с одинаковым характеристическим многочленом и собственными числами. Собственные же векторы тоже сохранят направления, но будут менять координаты (от базиса к базису), т. к. новый базис меняет «координатную сетку» векторого пространства. Наглядная тому иллюстрация есть в Примере 129, если Вы потеряли «нить» темы.
Но достаточно мозголомства, вернёмся к практике :)
Пример 139
Записать каноническое разложение матрицы 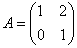
Заметьте, что в условии ничего не сказано о линейном преобразовании, и поэтому решение лучше оформлять в контексте заданного вопроса: найдём собственные значения матрицы. Для этого составим и решим характеристическое уравнение:
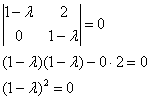
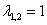 – в результате получены кратные (совпавшие) собственные числа. – в результате получены кратные (совпавшие) собственные числа.
Мысленно подставим 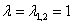 в определитель в определитель 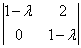 и запишем однородную систему линейных уравнений: и запишем однородную систему линейных уравнений:
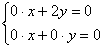
Что тут сказать? «Игрек» принудительно равен нулю: 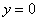 (иначе в первом уравнении получится неверное равенство). За «икс» можно принять любое ненулевое значение, в хорошем стиле положим, что (иначе в первом уравнении получится неверное равенство). За «икс» можно принять любое ненулевое значение, в хорошем стиле положим, что 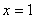 . Не ленимся и даже в таких простых случаях проверяем, что пара . Не ленимся и даже в таких простых случаях проверяем, что пара 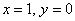 удовлетворяет каждому уравнению системы! удовлетворяет каждому уравнению системы!
Таким образом, кратным собственным числам соответствует одно множество коллинеарных векторов в «лице» собственного вектора 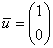 , и поэтому канонического разложения матрицы , и поэтому канонического разложения матрицы 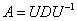 не существует. не существует.
Почему разложения 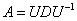 не существует?Потому что невозможно записать матрицу не существует?Потому что невозможно записать матрицу 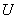 , которая должна состоять из двух линейно независимых собственных векторов. Размерность вектора равна двум («икс» и «игрек»), но сам-то вектор – один-одинёшенек. Коллинеарный товарищ, например , которая должна состоять из двух линейно независимых собственных векторов. Размерность вектора равна двум («икс» и «игрек»), но сам-то вектор – один-одинёшенек. Коллинеарный товарищ, например 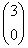 , в пару не годится (хотя бы по той причине, что , в пару не годится (хотя бы по той причине, что 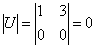 и обратной матрицы и обратной матрицы 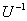 попросту не существует). попросту не существует).
Ответ: требуемое разложение неосуществимо.
Обратите внимание на корректность и точность ответа – нас никто не спрашивал о собственных значениях и собственных векторах. Кстати, об условии – его могут сформулировать и коварно: записать матрицу линейного преобразования 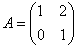 в базисе из собственных векторов. Коварство состоит в том, что здесь можно найти собственные числа и машинально дать нелегальный ответ в базисе из собственных векторов. Коварство состоит в том, что здесь можно найти собственные числа и машинально дать нелегальный ответ 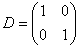 . Но базиса-то из собственных векторов не существует! . Но базиса-то из собственных векторов не существует!
И у этого примера есть простое геометрическое объяснение: матрица 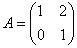 задаёт не что иное, как «перекос Джоконды», у которого существует лишь одно множество коллинеарных друг другу векторов, которые сохраняют направление в результате преобразования (и длину тоже, коль скоро задаёт не что иное, как «перекос Джоконды», у которого существует лишь одно множество коллинеарных друг другу векторов, которые сохраняют направление в результате преобразования (и длину тоже, коль скоро 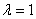 ). ).
И сейчас назрели важные вопросы:
 6.5.3. Сколько у матрицы собственных чисел и собственных векторов? 6.5.3. Сколько у матрицы собственных чисел и собственных векторов?
 6.5.1. Как найти собственные значения и собственные векторы? 6.5.1. Как найти собственные значения и собственные векторы?
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих
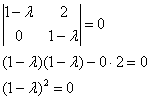
 6.5.3. Сколько у матрицы собственных чисел и собственных векторов?
6.5.3. Сколько у матрицы собственных чисел и собственных векторов? 6.5.1. Как найти собственные значения и собственные векторы?
6.5.1. Как найти собственные значения и собственные векторы?