6.4.1. Как записать оператор в матричной форме?
На этот счёт существует общее правило: чтобы записать матрицу линейного преобразования 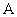 в в  -мерном базисе -мерном базисе 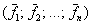 нужно последовательно и строго по порядку применять данный оператор к базисным векторам, а результаты заносить в столбцы матрицы (слева направо). нужно последовательно и строго по порядку применять данный оператор к базисным векторам, а результаты заносить в столбцы матрицы (слева направо).
Наш школьный случай 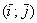 элементарен: сначала применим линейное преобразование элементарен: сначала применим линейное преобразование 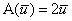 к первому базисному вектору: к первому базисному вектору: 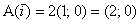 и запишем результат в 1-й столбец: и запишем результат в 1-й столбец: 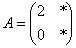 . Затем «обрабатываем» 2-й орт: . Затем «обрабатываем» 2-й орт: 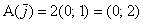 и заносим полученные координаты во 2-й столбец: и заносим полученные координаты во 2-й столбец:
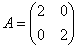 – матрица линейного преобразования – матрица линейного преобразования 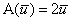 в базисе в базисе 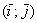 . .
Само же преобразование можно записать в виде функции 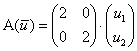 . .
! Не путаем обозначения: прямая буква 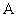 – оператор, косая буква – оператор, косая буква 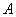 – матрица, не сильно это удачно, но практически общепринято в литературе. – матрица, не сильно это удачно, но практически общепринято в литературе.
Протестируем функцию на векторе 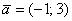 – выполним матричное умножение: – выполним матричное умножение:
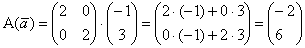 – в результате «на выходе» получены координаты вектора – в результате «на выходе» получены координаты вектора 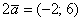 , что и требовалось проверить. , что и требовалось проверить.
Помимо векторов, оператор можно применить к любой точке плоскости. Для этого только нужно задать начало координат, получив тем самым декартову систему  . .
Поскольку любая точка плоскости 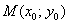 однозначно определяется её радиус-вектором однозначно определяется её радиус-вектором 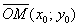 , то функция , то функция 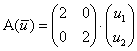 , по сути, применИма и для координат точек. Далее для простоты будем говорить и писАть, что, например, точка , по сути, применИма и для координат точек. Далее для простоты будем говорить и писАть, что, например, точка 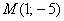
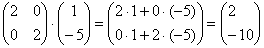 – перешла в точку – перешла в точку 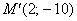 . .
И, наверное, Вы уже поняли, что делает этот оператор. Мысленно представьте произвольный треугольник на плоскости. После применения рассматриваемого линейного преобразования данный треугольник увеличится в два раза. Такие треугольники (имеющие равные соответствующие углы), как многие помнят из школы, называются подобными. Да и сам оператор носит такое же название:
Линейное преобразование 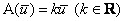 называется преобразованием подобия или гомотетией, причём: называется преобразованием подобия или гомотетией, причём:
– если 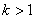 , то речь идёт об однородном растяжении (увеличении) объектов плоскости в , то речь идёт об однородном растяжении (увеличении) объектов плоскости в 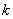 раз; раз;
– если 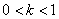 – то о сжатии (уменьшении) в – то о сжатии (уменьшении) в 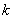 раз; раз;
– если 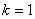 , то преобразование тождественно (ничего не меняет) , то преобразование тождественно (ничего не меняет)
– и если 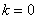 , то имеет место вырожденное преобразование. , то имеет место вырожденное преобразование.
В том случае, если 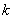 меньше нуля, то дополнительно к растяжению /сжатию / неизменности векторы меняют направление, а точки отображаются симметрично относительно начала координат. меньше нуля, то дополнительно к растяжению /сжатию / неизменности векторы меняют направление, а точки отображаются симметрично относительно начала координат.
Рассмотрим ещё несколько популярных примеров в системе  , и, чтобы разнообразить серые геометрические будни, мысленно нарисуем на координатной плоскости собачку. Можно и не мысленно! …Представили? Нарисовали? Отлично! , и, чтобы разнообразить серые геометрические будни, мысленно нарисуем на координатной плоскости собачку. Можно и не мысленно! …Представили? Нарисовали? Отлично!
Преобразование 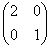 растягивает объекты плоскости по направлению вектора растягивает объекты плоскости по направлению вектора 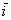 (горизонтали) в 2 раза, после чего Тузик радует нас своей широкой-широкой улыбкой! …Хотя, у многих, наверное, не Тузик…, да и не факт, что с улыбкой. Как сказал поэт, у каждого в голове своя морда =) (горизонтали) в 2 раза, после чего Тузик радует нас своей широкой-широкой улыбкой! …Хотя, у многих, наверное, не Тузик…, да и не факт, что с улыбкой. Как сказал поэт, у каждого в голове своя морда =)
И в самом деле, преобразуем точку 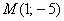 : :
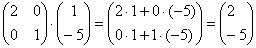 – «иксовая» координата увеличилась в 2 раза, а «игрековая» – не изменилась. – «иксовая» координата увеличилась в 2 раза, а «игрековая» – не изменилась.
Преобразование 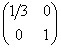 сожмёт собаку по горизонтали в 3 раза. Желающие могут по ходу объяснений приготовить мясорубку тестировать различные точки, выполняя матричное умножение, тут оно устное. сожмёт собаку по горизонтали в 3 раза. Желающие могут по ходу объяснений приготовить мясорубку тестировать различные точки, выполняя матричное умножение, тут оно устное.
Преобразование 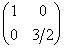 вытянет все ненулевые объекты плоскости по направлению вектора вытянет все ненулевые объекты плоскости по направлению вектора 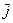 (по вертикали) в полтора раза. Получится очень удивлённый пёс. (по вертикали) в полтора раза. Получится очень удивлённый пёс.
Дополнительные знаки «минус» приведут к зеркальному отображению объектов (относительно оси ординат либо начала координат). И здесь я хочу остановиться на одном очень важном случае: преобразование 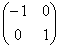 сохранит размеры, но отобразит все объекты плоскости симметрично относительно оси сохранит размеры, но отобразит все объекты плоскости симметрично относительно оси 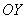 , частности, вектор , частности, вектор 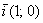 перейдёт в вектор перейдёт в вектор 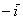 и базис и базис 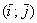 отобразится в другой, тоже ортонормированный базис отобразится в другой, тоже ортонормированный базис 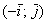 : :
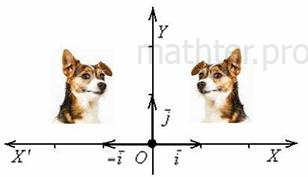
Это преобразование называют осевой или зеркальной симметрией. Такая симметрия характерна тем, что меняет ориентацию плоскости. Это проявляется в том, что как ни двигай по плоскости собачек – совместить их не удастся.
Ориентация бывает левой и правой. Вытяните перед собой обе руки ладонями вверх, так, чтобы большие пальцы смотрели в стороны под углом 90 градусов. При этом ваша правая рука моделирует правосторонний базис 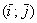 , где вектор , где вектор 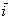 смотрит в направлении большого пальца, а смотрит в направлении большого пальца, а 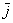 – в направлении указательного. Соответственно, левая рука аналогично моделирует левый базис – в направлении указательного. Соответственно, левая рука аналогично моделирует левый базис 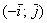 и левостороннюю ориентацию плоскости и левостороннюю ориентацию плоскости
Впрочем, оставим хлеб для геометрии, и вернёмся теме. Нетрудно догадаться, что преобразование 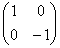 отобразит все объекты вниз – симметрично относительно оси отобразит все объекты вниз – симметрично относительно оси 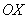 («отражение в реке»). («отражение в реке»).
Смотрим дальше:
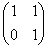 – образно говоря, «челюсть налево, уши направо». Это преобразование называется перекосом или сдвигом плоскости в направлении вектора – образно говоря, «челюсть налево, уши направо». Это преобразование называется перекосом или сдвигом плоскости в направлении вектора 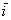 (в данном случае). (в данном случае).
И очевидна матрица вертикального сдвига 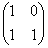 – в направлении вектора – в направлении вектора 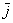 . .
Повороты:
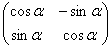 – данное преобразование поворачивает векторы системы – данное преобразование поворачивает векторы системы  против часовой стрелки на угол против часовой стрелки на угол  . .
И, наконец, все эти метаморфозы венчает общий случай 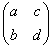 . Это преобразование переводит единичный квадрат с вершинами . Это преобразование переводит единичный квадрат с вершинами 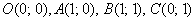 в параллелограмм с вершинами в параллелограмм с вершинами 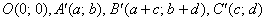 . И, разумеется, весь «рисунок» плоскости (вместе с квадратом) вытягивается в пропорциях этого параллелограмма. . И, разумеется, весь «рисунок» плоскости (вместе с квадратом) вытягивается в пропорциях этого параллелограмма.
! На всякий пожарный напомню, что координаты новых точек получаем по формуле  , где , где 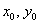 – координаты исходных. – координаты исходных.
Так, преобразование 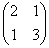 переводит единичный квадрат с синими вершинами (см. ниже) в зелёный параллелограмм с вершинами переводит единичный квадрат с синими вершинами (см. ниже) в зелёный параллелограмм с вершинами 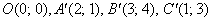 : :
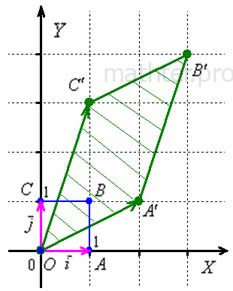
При этом координатный вектор 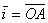 , отображается в вектор , отображается в вектор 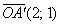 , а вектор , а вектор 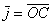 – в вектор – в вектор 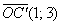 . ПосмотрИте на координаты полученных векторов и на числа матрицы преобразования ;) . ПосмотрИте на координаты полученных векторов и на числа матрицы преобразования ;)
Нетрудно понять, что масштабируется и площадь – была площадь квадрата 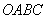 , равная единице, а стала – площадь параллелограмма , равная единице, а стала – площадь параллелограмма 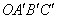 . Причём, площадь этого параллелограмма по модулю в точности равна определителю матрицы преобразования. В нашем случае: . Причём, площадь этого параллелограмма по модулю в точности равна определителю матрицы преобразования. В нашем случае: 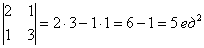
Если же определитель отрицателен, то такое преобразование не только искажает объекты плоскости (в общем случае), но и выполняет их отражение (меняет ориентацию). Так, для преобразования 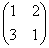 получаем вроде бы тот же параллелограмм…, да не тот! Самостоятельно проанализируйте, куда отображаются точки получаем вроде бы тот же параллелограмм…, да не тот! Самостоятельно проанализируйте, куда отображаются точки 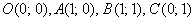 , и вы поймёте, что помимо искажения (в таких же пропорциях, что и первое преобразование), выполняется ещё и отражение Тузика «наоборот». О чём говорит знак определителя: , и вы поймёте, что помимо искажения (в таких же пропорциях, что и первое преобразование), выполняется ещё и отражение Тузика «наоборот». О чём говорит знак определителя: 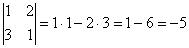 . .
И теперь самое время прояснить геометрический смысл определителя. Определитель «два на два» 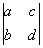 по модулю: по модулю: 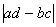 – есть площадь параллелограмма, построенного на векторах – есть площадь параллелограмма, построенного на векторах 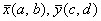 (см. рис. выше). Определитель «3 на 3» (см. рис. выше). Определитель «3 на 3»  по модулю – есть объём параллелепипеда, построенного на векторах по модулю – есть объём параллелепипеда, построенного на векторах 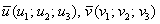 , , 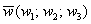 (см. смешанное произведение векторов). И для бОльших размеров (4 на 4 и выше) можно говорить об объеме абстрактного n-мерного параллелепипеда. (см. смешанное произведение векторов). И для бОльших размеров (4 на 4 и выше) можно говорить об объеме абстрактного n-мерного параллелепипеда.
Если определитель матрицы преобразования равен нулю 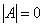 , то оно является вырожденным. Так, вырождено тривиальное нулевое преобразование, которое отображает все векторы в нулевой вектор. Это преобразование имеет нулевую матрицу, для двумерного случая: , то оно является вырожденным. Так, вырождено тривиальное нулевое преобразование, которое отображает все векторы в нулевой вектор. Это преобразование имеет нулевую матрицу, для двумерного случая: 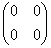 . Или, например, оператор . Или, например, оператор 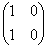 , переводящий векторы , переводящий векторы 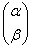 в коллинеарные друг другу векторы в коллинеарные друг другу векторы 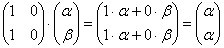 . .
Эффект вырожденного преобразования состоит в потере информации, и, как следствие, невозможности осуществления обратного преобразования. Так, если нам предъявить готовый результат 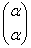 из последнего примера, то невозможно выяснить, какой именно вектор из последнего примера, то невозможно выяснить, какой именно вектор 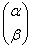 подвергся преобразованию. подвергся преобразованию.
Типичное вырожденное преобразование – это проецирование. Говоря проще, если вы видите тень в форме круга, то далеко не факт, что её отбрасывает шар. Это может быть эллипсоид, цилиндр, зонтик – много какие объекты. Но то уже пример из пространства.
И следующее утверждение давно читалось «между строк»: любое линейное преобразование 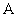 n-мерного векторного пространства можно записать в виде квадратной матрицы n-мерного векторного пространства можно записать в виде квадратной матрицы 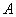 размером размером 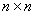 – в некотором фиксированном базисе – в некотором фиксированном базисе 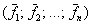 этого пространства. этого пространства.
Верно и обратное: любой квадратной матрице 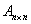 соответствует определённое линейное преобразование этого пространства, записанное в базисе соответствует определённое линейное преобразование этого пространства, записанное в базисе 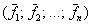 . .
В частности, любое преобразование плоскости можно записать в виде матрицы 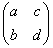 в базисе в базисе 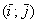 , и обратно – любой матрице «два на два» соответствует определённое преобразование плоскости, записанное в этом базисе. , и обратно – любой матрице «два на два» соответствует определённое преобразование плоскости, записанное в этом базисе.
Эти факты хоть и очевидны, но строго доказаны в теории.
Переходим к практическим задачам:
Пример 131
Линейный оператор задан матрицей 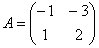 . Найти образ вектора . Найти образ вектора 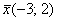 . Используя обратное преобразование, выполнить проверку. . Используя обратное преобразование, выполнить проверку.
Но прежде, инструктаж перед полётом.
Во-первых, не вкладываем в векторы и в само преобразование никакой смысл: ни геометрический, ни химический, ни алхимический – никакой. Коль скоро об этом не сказано в условии. Никаких базисов. «Не болтаем» и оформляем решение абстрактно.
Во-вторых, вспоминаем терминологию: образ – это то, что получается в результате преобразования, а прообраз – это исходный объект, вектор 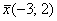 в нашем случае. в нашем случае.
Решение: найдём вектор 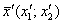 , полученный в результате преобразования вектора , полученный в результате преобразования вектора 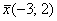 . Это мы уже неоднократно делали выше: . Это мы уже неоднократно делали выше:
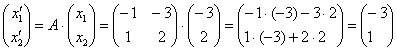
Таким образом, это линейное преобразование перевело вектор 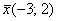 (прообраз) в вектор (прообраз) в вектор 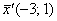 (образ). (образ).
Теперь найдём обратное преобразование, которое превращает образы векторов – обратно в их прообразы. Оно существует лишь в том случае, если прямое преобразование не вырождено. Проверяем этот факт: 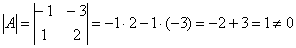 , значит, преобразование не вырождено и обратное преобразование осуществимо. , значит, преобразование не вырождено и обратное преобразование осуществимо.
Запишем матричную функцию в виде 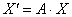 , где , где 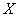 – координатный столбец прообразов, а – координатный столбец прообразов, а 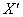 – образов. Этой функцией мы только что воспользовались для нахождения вектора – образов. Этой функцией мы только что воспользовались для нахождения вектора 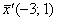 . Но теперь нам нужно выразить прообраз. Чтобы выразить . Но теперь нам нужно выразить прообраз. Чтобы выразить 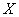 , умножим обе части на обратную матрицу , умножим обе части на обратную матрицу 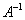 слева: слева:
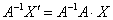
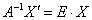 , откуда следует, что , откуда следует, что
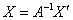
Таким образом, обратному линейному преобразованию соответствует обратная матрица 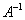 . Осталось её найти. Это можно сделать «традиционным» способом либо с помощью элементарных преобразований. Здесь я рекомендую первый путь, поскольку он позволяет сразу выяснить, а существует ли матрица . Осталось её найти. Это можно сделать «традиционным» способом либо с помощью элементарных преобразований. Здесь я рекомендую первый путь, поскольку он позволяет сразу выяснить, а существует ли матрица 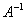 вообще. Тем более, это мы уже сделали: вообще. Тем более, это мы уже сделали: 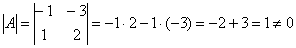 , значит, обратное линейное преобразование существует и задаётся матрицей , значит, обратное линейное преобразование существует и задаётся матрицей 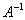 . .
Здесь и далее я не буду подробно расписывать процесс нахождения обратной матрицы, ограничиваясь готовым результатом. Итак, в результате стандартных действий находим 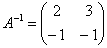 и выясняем, во что обратится найденный вектор и выясняем, во что обратится найденный вектор 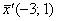 : :
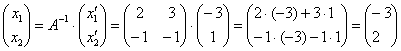 – получены координаты исходного вектора – получены координаты исходного вектора 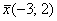 (прообраза), что и требовалось проверить. (прообраза), что и требовалось проверить.
Ответ: 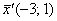
Небольшая задачка для разминки:
Пример 132
В результате применения оператора, заданного матрицей 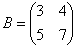 , получены образы , получены образы 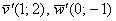 . Найти прообразы данных векторов. . Найти прообразы данных векторов.
Сверяемся и повышаем размерность:
Пример 133
Даны два линейных преобразования:
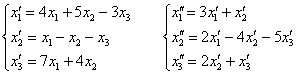
Средствами матричного исчисления найти преобразование, выражающее 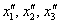 через через 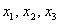 . .
…Спокойно, спокойно, сейчас во всём разберёмся…
Решение: и первое, что здесь опять можно сказать – это отсутствие информации о характере векторов 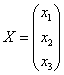 . Понятно только, что они заданы в некотором базисе трёхмерного векторого пространства, ибо матрица линейного преобразования (замаскированная в виде системы) порождается базисом. Он нам тоже не известен, но для решения задачи эта информация и не нужна. . Понятно только, что они заданы в некотором базисе трёхмерного векторого пространства, ибо матрица линейного преобразования (замаскированная в виде системы) порождается базисом. Он нам тоже не известен, но для решения задачи эта информация и не нужна.
Тем не менее, для пущего понимания вновь обратимся к геометрии и предположим, что все дела происходят в обычной декартовой системе координат  . И, чтобы не прослыть живодёром, я рассмотрю 3D-модель кота Леопольда =) . И, чтобы не прослыть живодёром, я рассмотрю 3D-модель кота Леопольда =)
Запишем матрицу первого преобразования: 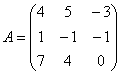 . Данное преобразование переводит векторы . Данное преобразование переводит векторы 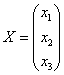 в образы в образы 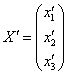 . Систему, кстати, удобнее переписать в виде уже знакомой матричной функции: . Систему, кстати, удобнее переписать в виде уже знакомой матричной функции:
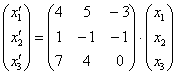 или, если короче: или, если короче: 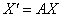 . .
Данный оператор определённым образом преобразует все векторы (а значит и точки) пространства. Геометрически это означает, что кот Леопольд, оказывается, например, сплющенным (не знаю, не проверял).
Теперь ОЧЕНЬ ВНИМАТЕЛЬНО записываем матрицу второго преобразования: 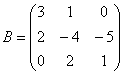 (здесь существует немалый риск поставить ноль не там где нужно). Данное преобразование переводит векторы (здесь существует немалый риск поставить ноль не там где нужно). Данное преобразование переводит векторы 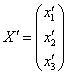 в образы в образы 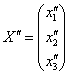 , в результате чего «сплющенный кот», скажем, растягивается вдоль какой-нибудь плоскости. , в результате чего «сплющенный кот», скажем, растягивается вдоль какой-нибудь плоскости.
Аналогично – запишем преобразование в матричной форме:
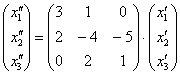 или: или: 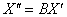
По условию, нужно найти преобразование, выражающее 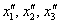 через через 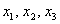 , то есть результирующее преобразование (композицию), которое нам сразу даст «сплющенного и растянутого Леопольда». Для этого подставим , то есть результирующее преобразование (композицию), которое нам сразу даст «сплющенного и растянутого Леопольда». Для этого подставим 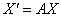 в уравнение в уравнение 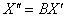 : :
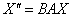
И всё оказывается до безобразия просто – главное, матрицы перемножить в правильном порядке. Вычислим матрицу композиционного преобразования:
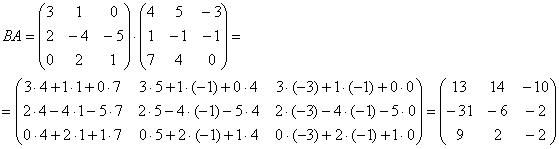
распишем итоговую функцию 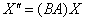 : :
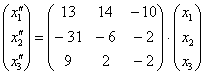
и осуществим матричное умножение в правой части:
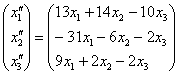
Две матрицы равны, если равны их соответствующие элементы. Таким образом, итоговое преобразование, выражающее координаты векторов-образов 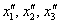 через координаты векторов-прообразов через координаты векторов-прообразов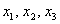 , запишется в виде следующей системы: , запишется в виде следующей системы:
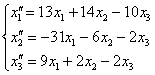
Проверка: подставим уравнения 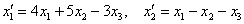 , , 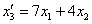 левой системы (см. условие) в правую часть каждого уравнения правой системы: левой системы (см. условие) в правую часть каждого уравнения правой системы:
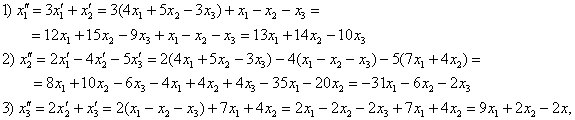
что и требовалось проверить.
«Проверочный» способ, кстати, можно было бы рискнуть взять и за основной, если бы итоговое преобразование не требовалось найти средствами матричного исчисления.
Да, и не забываем записать
ответ: 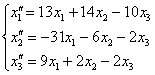
Как пользоваться этой системой? Очень просто – берём, например, вектор 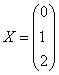 и тупо подставляем его координаты в систему: и тупо подставляем его координаты в систему:
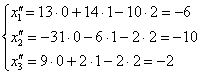 – таким образом, он перешёл в вектор – таким образом, он перешёл в вектор 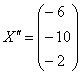 . .
Более академичный способ – использование матричного уравнения 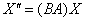 : :
Если преобразования, заданные матрицами  , ,  , не вырождены (не проверял), то «кота можно ввернуть к первоначальному виду». Для этого нужно найти обратную матрицу результирующего преобразования , не вырождены (не проверял), то «кота можно ввернуть к первоначальному виду». Для этого нужно найти обратную матрицу результирующего преобразования 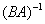 и воспользоваться функцией и воспользоваться функцией 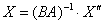 . .
Творческое задание для самостоятельного исследования:
Пример 134
Даны линейные преобразования:
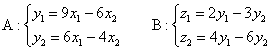
Найти образ вектора 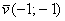 двумя способами: двумя способами:
1) путём последовательного применения преобразований 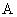 и и 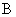 ; ;
2) с помощью композиционного оператора, выражающего 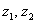 через через 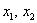 . .
Был велик соблазн вас запутать, но всё же я воздержался. Однако на практике нужно иметь в виду следующее:
– системы запросто могут быть переставлены местами;
– условие задачи может требовать выразить 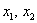 через через 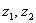 и тогда потребуется дополнительно находить обратную матрицу результирующего преобразования. и тогда потребуется дополнительно находить обратную матрицу результирующего преобразования.
В этой связи очень важно РАЗОБРАТЬСЯ в сути задания, и если что-то осталось недопонятым, обязательно перечитайте объяснения ещё раз, можно даже порисовать.
Да, и стиль напомню: прямые буквы 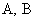 – операторы, косые – операторы, косые 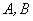 – матрицы. – матрицы.
 6.4.2. Матрица линейного преобразования в различных базисах 6.4.2. Матрица линейного преобразования в различных базисах
 6.4. Линейные преобразования 6.4. Линейные преобразования
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих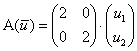 .
.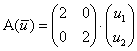 , по сути, применИма и для координат точек. Далее для простоты будем говорить и писАть, что, например, точка
, по сути, применИма и для координат точек. Далее для простоты будем говорить и писАть, что, например, точка 
 , где
, где 
 по модулю – есть объём параллелепипеда, построенного на векторах
по модулю – есть объём параллелепипеда, построенного на векторах 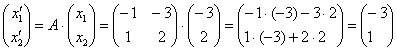
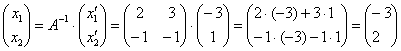 – получены координаты исходного вектора
– получены координаты исходного вектора 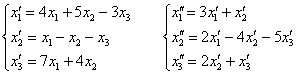
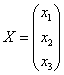 . Понятно только, что они заданы в некотором
. Понятно только, что они заданы в некотором 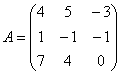 . Данное преобразование переводит векторы
. Данное преобразование переводит векторы 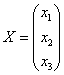 в образы
в образы 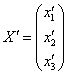 . Систему, кстати, удобнее переписать в виде уже знакомой матричной функции:
. Систему, кстати, удобнее переписать в виде уже знакомой матричной функции: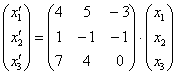 или, если короче:
или, если короче: 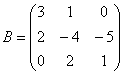 (здесь существует немалый риск поставить ноль не там где нужно). Данное преобразование переводит векторы
(здесь существует немалый риск поставить ноль не там где нужно). Данное преобразование переводит векторы 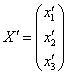 в образы
в образы 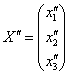 , в результате чего «сплющенный кот», скажем, растягивается вдоль какой-нибудь плоскости.
, в результате чего «сплющенный кот», скажем, растягивается вдоль какой-нибудь плоскости.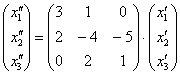 или:
или: 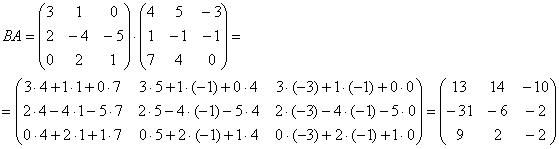
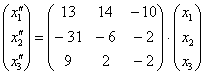
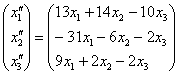
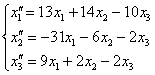
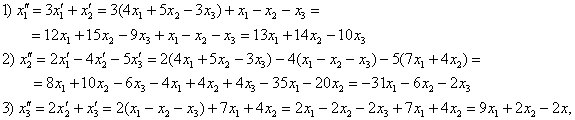
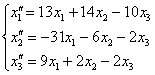
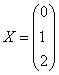 и тупо подставляем его координаты в систему:
и тупо подставляем его координаты в систему: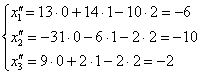 – таким образом, он перешёл в вектор
– таким образом, он перешёл в вектор 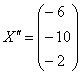 .
.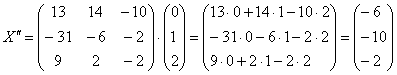
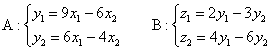
 6.4.2. Матрица линейного преобразования в различных базисах
6.4.2. Матрица линейного преобразования в различных базисах 6.4. Линейные преобразования
6.4. Линейные преобразования