6.4.2. Матрица линейного преобразования в различных базисах
Как мы выяснили ранее, матрица линейного преобразования порождается базисными векторами. Но базисов существует очень много! (в том или ином векторном пространстве). И из этого следует, что одно и то же линейное преобразование 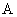 в разных базисах в общем случае имеет разные матрицы. в разных базисах в общем случае имеет разные матрицы.
Так, мы рассмотрели матрицу 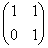 перекоса плоскости в направлении вектора перекоса плоскости в направлении вектора 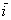 в декартовой системе в декартовой системе 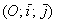 . Но на плоскости можно задать несчётное множество аффинных («косоугольных») систем . Но на плоскости можно задать несчётное множество аффинных («косоугольных») систем 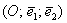 , где , где 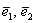 – произвольные неколлинеарные векторы. И тот же самый перекос запишется совершенно другой матрицей – в зависимости от того, какие векторы мы выбрали в качестве базиса. – произвольные неколлинеарные векторы. И тот же самый перекос запишется совершенно другой матрицей – в зависимости от того, какие векторы мы выбрали в качестве базиса.
Следующие задачи посвящены вопросам взаимосвязи матриц одного и того же линейного преобразования в разных базисах, после чего я приведу общие формулы:
Пример 135
Линейный оператор задан матрицей 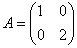 в базисе в базисе 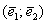 . Найти матрицу этого преобразования в базисе . Найти матрицу этого преобразования в базисе 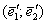 , если , если 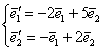
Решение: в условии опять ничего не сказано о природе векторов, но зато бросается в глаза линейное преобразование. Коль скоро речь идёт о некоем базисе 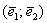 , то любой вектор двумерного пространства раскладывается по этому базису , то любой вектор двумерного пространства раскладывается по этому базису 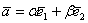 , и линейный оператор , и линейный оператор 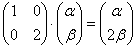 – удваивает его вторую координату. – удваивает его вторую координату.
Для наглядности снова предположим, что это геометрические векторы и базис. Тогда предложенное линейное преобразование вытягивает все ненулевые объекты плоскости в направлении координатного вектора 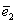 в 2 раза, и наша задача состоит в том, чтобы записать матрицу в 2 раза, и наша задача состоит в том, чтобы записать матрицу 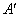 этого же преобразования в новом базисе этого же преобразования в новом базисе 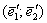 . .
Для решения данного вопроса существует специальная формула:
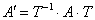 , где , где 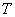 – матрица перехода от базиса – матрица перехода от базиса 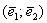 к базису к базису 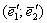 . .
Составляется она просто: берём вектор 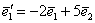 и «укладываем» коэффициенты его разложения в 1-й столбец (!) матрицы: и «укладываем» коэффициенты его разложения в 1-й столбец (!) матрицы: 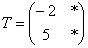 . Затем рассматриваем вектор . Затем рассматриваем вектор 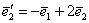 и заносим коэффициенты его разложения во 2-й столбец: и заносим коэффициенты его разложения во 2-й столбец:
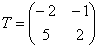
Внимание! Базисные векторы, в данном случае 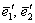 , следует «перебирать» строго по порядку! , следует «перебирать» строго по порядку!
Остальное дело техники.
Находим обратную матрицу 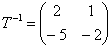 , произведение: , произведение:
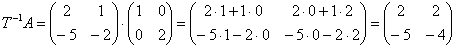
и, наконец, матрицу рассматриваемого линейного преобразования в новом базисе:
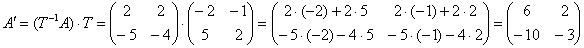
Пользуясь ассоциативностью матричного умножения, сначала можно найти 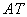 , а затем , а затем 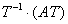 , но, в общем-то, это уже несущественные детали. , но, в общем-то, это уже несущественные детали.
Ответ: 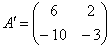
Ещё раз повторим смысл задания: само линейное преобразование не поменялось – оно по-прежнему растягивает ненулевые объекты плоскости вдоль «старого» вектора 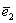 в 2 раза и не деформирует их в направлении вектора в 2 раза и не деформирует их в направлении вектора 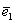 , но в новом базисе , но в новом базисе 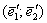 матрица данного преобразования уже другая. И вы видите её в ответе. матрица данного преобразования уже другая. И вы видите её в ответе.
Очевидно, что найденная матрица 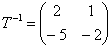 задаёт обратное преобразование, т. е. выражает старые базисные векторы через новые. Аккуратно «транспонируем» столбцы матрицы в коэффициенты соответствующей системы: задаёт обратное преобразование, т. е. выражает старые базисные векторы через новые. Аккуратно «транспонируем» столбцы матрицы в коэффициенты соответствующей системы: 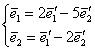 . .
Таким образом, при желании всегда можно вернуться к матрице преобразования в старом базисе: 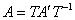 (выполнив, кстати, проверку). Эта формула следует из простых логических соображений, но её можно вывести и формально – разрешив матричное уравнение (выполнив, кстати, проверку). Эта формула следует из простых логических соображений, но её можно вывести и формально – разрешив матричное уравнение 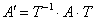 относительно относительно 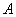 . .
Какой базис удобнее? Ну конечно, 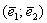 , где матрица преобразования имеет вид , где матрица преобразования имеет вид 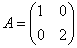 , и сразу виднА характерная особенность этого преобразования. Следует заметить, что на практике как раз и стараются отыскать такой особый базис, чем мы займёмся в ближайшем будущем. Пока же всё вышло наоборот :) , и сразу виднА характерная особенность этого преобразования. Следует заметить, что на практике как раз и стараются отыскать такой особый базис, чем мы займёмся в ближайшем будущем. Пока же всё вышло наоборот :)
Трехмерный случай для самостоятельного решения:
Пример 136
Найти матрицу линейного преобразования в базисе 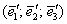 , где , где 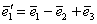 , , 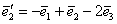 , , 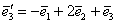 , если она задана в базисе , если она задана в базисе 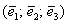 : :
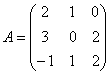
Не помешает проверка по формуле 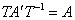 , где , где 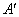 – найденная матрица, благо, Матричный калькулятор приложен к Книге. – найденная матрица, благо, Матричный калькулятор приложен к Книге.
Теперь обещанный общий случай и крайне интересные факты из теории: пусть невырожденное линейное преобразование 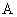 задано матрицами задано матрицами 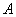 и и 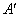 в произвольных базисах в произвольных базисах 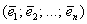 и и 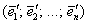 n-мерного линейного пространства. Тогда эти матрицы связаны отношением n-мерного линейного пространства. Тогда эти матрицы связаны отношением 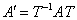 , где , где  – матрица перехода к базису – матрица перехода к базису 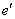 , составленная из координат векторов , составленная из координат векторов 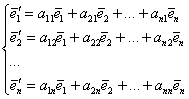 . .
Матрицы 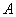 и и 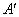 , представимые в виде , представимые в виде 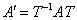 называют подобными. И у таких матриц есть несколько инвариантов. В курсе геометрии сиё понятие уже встречалось: инвариант – это величина, которая не меняется в результате преобразования. называют подобными. И у таких матриц есть несколько инвариантов. В курсе геометрии сиё понятие уже встречалось: инвариант – это величина, которая не меняется в результате преобразования.
Так, определители подобных матриц равны: 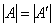 . И в самом деле, рассмотрим матрицы . И в самом деле, рассмотрим матрицы 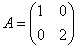 , , 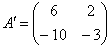 из Примера 135 и вычислим их определители: из Примера 135 и вычислим их определители:
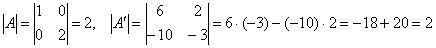 , ч. т. п. , ч. т. п.
Другой инвариант – след матрицы: 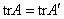 (англ. trace – след). Напоминаю, что это сумма элементов главной диагонали: (англ. trace – след). Напоминаю, что это сумма элементов главной диагонали: 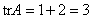 и и 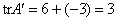 . .
Данные факты можно использовать для «быстрой» проверки решения, в частности, Примера 136. Хотя, это, конечно, не железобетон.
Любой паре подобных матриц соответствует определённое линейное преобразование, и скоро мы узнАем его другие, более важные инварианты.
 6.5. Собственные числа и собственные векторы линейного преобразования 6.5. Собственные числа и собственные векторы линейного преобразования
 6.4.1. Как записать оператор в матричной форме? 6.4.1. Как записать оператор в матричной форме?
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих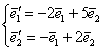
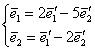 .
. 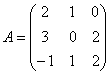
 – матрица перехода к базису
– матрица перехода к базису 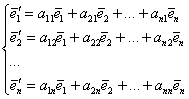 .
. 6.5. Собственные числа и собственные векторы линейного преобразования
6.5. Собственные числа и собственные векторы линейного преобразования 6.4.1. Как записать оператор в матричной форме?
6.4.1. Как записать оператор в матричной форме?