|
Ваш репетитор, справочник и друг!
|
6.5.3. Сколько у матрицы собственных чисел и собственных векторов?Что касаемо количества собственных чисел, то всё просто: у матрицы Случай первый: они комплексные. Простейший пример: Оно имеет сопряжённые комплексные корни Случай второй, самый распространённый. Собственные числа матрицы Случай третий, самый интересный. Среди собственных чисел есть кратные, или же только кратные, как в Примере 139. В этой ситуации неколлинеарных собственных векторов может оказаться… сколько угодно! Меньше, чем собственных чисел (недавний Пример 139). Может оказаться ровно А может – вообще бесконечно много! Например, поворот плоскости на 180 градусов. Ему соответствует матрица Следует отметить, что этот поворот – частный случай преобразования подобия, и у гомотетии, к слову, тоже, любой ненулевой вектор – собственный, а коэффициент подобия Однако не будем увлекаться геометрией и продолжим нарабатывать практику. Задачи с матрицей «три на три» отличаются бОльшей технической сложностью: Пример 140 Найти собственные векторы линейного преобразования, заданного матрицей Решение: по условию, требуется найти собственные векторы, но алгоритм таков, что в первую очередь всё равно нужно найти собственные числа. Вычтем «лямбду» из всех чисел главной диагонали матрицы Определитель раскроем по первому столбцу: На этом месте немного притормозим и познакомимся с очень полезным техническим приёмом, который значительно упростит дальнейшую жизнь. Практически во всех методических пособиях вам будет предложено раскрыть все скобки, получить слева многочлен 3-й степени и стать жертвой долгих мытарств. За годы практики я отработал рациональную схему, позволяющую избежать этих неприятностей: Сначала представим в виде произведения «хвост» левой части: Выполненное действие не привело к заметному результату, поэтому пробуем разложить на множители квадратный трёхчлен Вынесем Решаем ещё одно квадратное уравнение, в итоге: Не тушуйтесь, это была самая длинная ветка алгоритма, в большинстве случаев произведение получается значительно быстрее. Собственные значения всегда стараемся расположить в порядке возрастания: Теперь ищем собственные векторы, и это тоже небольшая мыльная опера: 1) Мысленно либо на черновике подставим значение Систему обычно решают методом Гаусса, но здесь быстрее срабатывает «школьный» способ. Из 3-го уравнения выразим Поскольку первая координата нулевая, то получаем систему И снова обратите внимание на обязательное наличие линейной зависимости. Если получается только тривиальное решение Итак, Собственный вектор: И ещё раз – проверяем, что найденное решение 2) Для собственного значения Из 2-го уравнения системы выразим Поскольку «зетовая» координата равна нулю, то получаем систему Проверяем, что значения 3) И, наконец, собственному значению Второе уравнение выглядит самым простым, поэтому из него выразим Всё путём – из обоих уравнений вышла линейная зависимость В результате «икс» и «игрек» оказались выражены через «зет»: Положим Проверяем, что трофеи Ответ: собственные векторы: Повторим смысл: эти векторы задают три различных пространственных «коридора», в которых линейное преобразование, заданное матрицей Так как собственные числа действительны и различны, то векторы Задача с более простыми вычислениями для самостоятельного решения: Пример 141 Найти собственные векторы линейного преобразования, заданного матрицей При нахождении собственных чисел постарайтесь не доводить дело до многочлена 3-й степени (см. Пример 140). Системы можно решать разными путями – здесь нет однозначности. Векторы, которые вы найдёте, могут отличаться от векторов образца с точностью до пропорциональности их соответствующих координат, а-ка
|
|
© mathprofi.ru - mathter.pro, 2010-2025, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих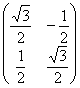 и составим
и составим 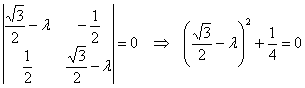
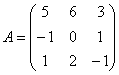
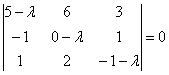
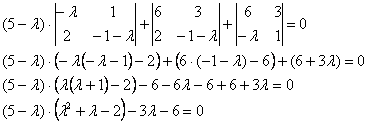
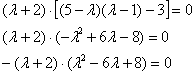
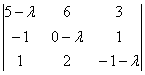 , с которого «снимем» коэффициенты
, с которого «снимем» коэффициенты 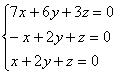
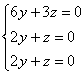 , из каждого уравнения которой следует, что
, из каждого уравнения которой следует, что 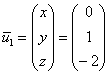
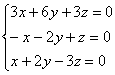
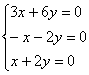 , из каждого уравнения которой следует линейная зависимость
, из каждого уравнения которой следует линейная зависимость 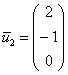 .
.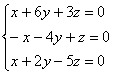
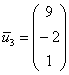 .
.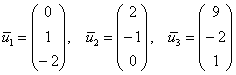
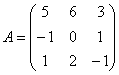 , переводит векторы в коллинеарные им векторы с коэффициентами
, переводит векторы в коллинеарные им векторы с коэффициентами 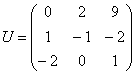 – матрица перехода к базису из собственных векторов (в столбцах их координаты), а
– матрица перехода к базису из собственных векторов (в столбцах их координаты), а 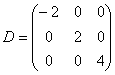 – матрица данного линейного преобразования в базисе из собственных векторов. Осталось только
– матрица данного линейного преобразования в базисе из собственных векторов. Осталось только 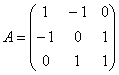
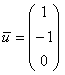 и
и 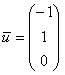 . Эстетичнее выбрать
. Эстетичнее выбрать 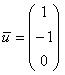 , но ничего страшного, если остановитесь и на втором варианте. Однако всему есть разумные пределы, и версия
, но ничего страшного, если остановитесь и на втором варианте. Однако всему есть разумные пределы, и версия 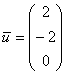 смотрится уже не айс. Примерный чистовой образец оформления задания в конце книги.
смотрится уже не айс. Примерный чистовой образец оформления задания в конце книги. 6.5.4. Как решать задачу в случае кратных собственных чисел?
6.5.4. Как решать задачу в случае кратных собственных чисел? 6.5.2. Линейное преобразование в базисе из собственных векторов
6.5.2. Линейное преобразование в базисе из собственных векторов