|
Ваш репетитор, справочник и друг!
|
6.5.4. Как решать задачу в случае кратных собственных чисел?Общий алгоритм остаётся прежним, но здесь есть свои особенности, и некоторые участки решения целесообразно выдержать в более строгом стиле: Пример 142 Найти собственные числа и собственные векторы матрицы Это эквивалентная формулировка задания, поскольку каждой квадратной матрице соответствует своё линейное преобразование (в некотором фиксированном базисе). Решение: составим и решим характеристическое уравнение: И тут, конечно же, оприходуем сказочный первый столбец: Дальше тоже всё сказочно: И, после разложения квадратного трёхчлена на множители: В результате получены собственные числа Найдем собственные векторы: 1) С одиноким солдатом Из последних двух уравнений четко просматривается равенство Собственный вектор: 2-3) Теперь снимаем пару часовых. В случае двух совпавших собственных чисел может получиться либо два, либо один собственный вектор. Невзирая на кратность корней, подставим значение А теперь факт: собственные векторы – это в точности векторы фундаментальной системы решений. Собственно, в предыдущих примерах мы только и занимались тем, что находили векторы фундаментальной системы. Просто до сего момента данный термин особо не требовался. Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду: Придерживаемся стандартной схемы решения однородной системы: Выразим базисную переменную через свободные переменные: В контексте нашей задачи общее решение удобнее записать не в строку, а в столбец: Примечание: искушенные читатели могут подобрать данные векторы и устно – просто глядя на систему И после столь полезной информации запишем Аналогичный пример для самостоятельного решения: Пример 143 Найти собственные числа и собственные векторы Примерный образец чистового оформления в конце книги. В Примерах 142, 143 количество собственных векторов оказалось равно количеству собственных чисел, поэтому исходная матрица представима в каноническом виде Пример 144 Найти собственные числа и собственные значения матрицы Решение: составим и решим характеристическое уравнение: Определитель раскроем по первому столбцу: Дальнейшие упрощения проводим согласно рассмотренной методике, избегая многочлена 3-й степени: Найдем собственные векторы: 1) С корнем Из 3-го уравнения выразим Положим Собственный вектор: 2-3) Для кратных значений Запишем матрицу системы и методом Гаусса приведём её к ступенчатому виду: Переменные Ответ: Очевидно, здесь невозможно представить матрицу в виде Следующее задание…, да нет, пожалуй, достаточно :) И я поздравляю Вас с успешным (надеюсь) освоением курса! Дополнительные источники информации я уже рекомендовал в конце параграфа о евклидовом пространстве. Также в рамках блога мы обсуждаем доступную литературу, и не только, разумеется, по алгебре. ...И что-то мне подсказывает, что многие воодушевились! В самом начале я открыл Вам Врата алгебры, чтобы заботливо сопроводить до другой двери:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих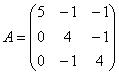
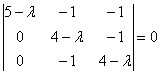
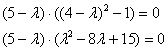
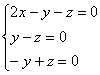
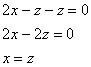
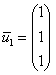
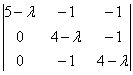 , который приносит нам следующую
, который приносит нам следующую 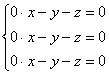
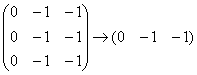 – единственное действие состояло в удалении лишних пропорциональных строк.
– единственное действие состояло в удалении лишних пропорциональных строк.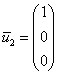 ;
;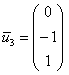 .
.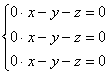 . Но это если случай простой. Кроме того, можно «углядеть» и другой набор собственных векторов, например:
. Но это если случай простой. Кроме того, можно «углядеть» и другой набор собственных векторов, например: 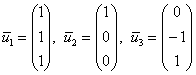 .
.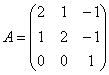
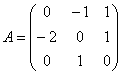
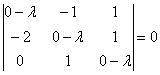
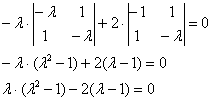
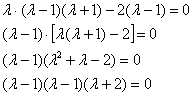
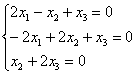
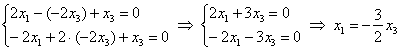 .
. 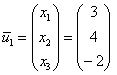
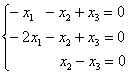 .
.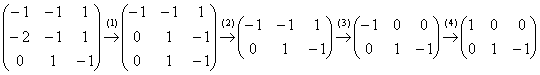
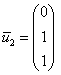
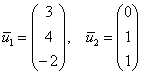 .
. 6.6. Гомоморфизм алгебраических структур
6.6. Гомоморфизм алгебраических структур 6.5.3. Сколько у матрицы собственных чисел и собственных векторов?
6.5.3. Сколько у матрицы собственных чисел и собственных векторов?