|
Ваш репетитор, справочник и друг!
|
5.7. Задача с треугольной пирамидойКонцептуально эта задача напоминает задачу с треугольником на плоскости. Только вот треугольников у нас теперь
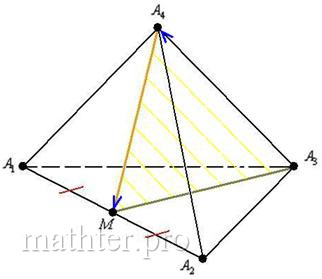
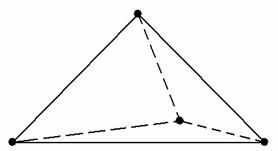
четыре, и образуют они треугольную пирамиду или тетраэдр: У треугольной пирамиды есть: – четыре вершины; – шесть рёбер (сторон); – четыре грани. Чем богаты, тем и рады. Не буду перечислять геометрические свойства данной фигуры, известные из школьной программы, поскольку аналитическую геометрию интересует совсем другое, а именно: уравнения рёбер, плоскостей, всевозможные длины, углы и некоторые другие вещи, которые вы увидите прямо сейчас. Типовая задача формулируется так: Задача 166 Треугольная пирамида задана координатами своих вершин, пусть это будут вершины 1) найти длину ребра 2) составить уравнения стороны 3) найти угол между рёбрами 4) найти площадь грани 5) найти угол между ребром 6) составить уравнение грани 7) составить уравнения высоты 8) вычислить длину высоты 9) найти основание высоты 10) вычислить объем пирамиды; 11) составить уравнения медианы 12) составить уравнение плоскости, проходящей через прямую 13) найти угол между плоскостями 14) выполнить чертёж пирамиды 15) перекреститься левой пяткой. Во-первых, разберёмся с обозначениями вершин. Самый распространённый вариант, когда они обозначены буквами А всё это я сказал к тому, что в вашей задаче могут быть совершенно другие обозначения вершин. Например, В этой связи очень важно выполнить схематический рисунок пирамиды, чтобы не запутаться в дальнейшем алгоритме решение. Да, более подготовленные читатели могут представлять тетраэдр мысленно, но для «чайников» чертёж просто обязателен. Итак, на предварительном этапе разбираемся с обозначениями вершин, анализируем условие, находим «особенную» плоскость и точку и выполняем бесхитростный набросок на черновике. С чего начать решение? Начать лучше всего с того, что загнать координаты вершин в Геометрический калькулятор (см. приложения), который автоматически рассчитает наиболее популярные пункты. Ибо приятно заранее знать правильные ответы ;) Но расписать-то всё нужно подробно. И поэтому оформление решения удобно начать с нахождения векторов. Почти всегда векторы
откладываются от первой вершины, в данном случае – от точки Чтобы комфортнее воспринимать информацию, координаты четырёх точек и трёх полученных вектора рекомендую переписать на отдельный листочек. Это же сделайте, когда будете решать свою задачу – чтобы каждый раз не выискивать нужный вектор, нужную точку. Их удобно держать перед глазами. Понеслось: 1) Найдём длину ребра Я обычно округляю результаты до двух знаков после запятой, но в условии задачи может быть дополнительное указание проводить округления, например, до 1 или 3 десятичных знаков. Полагаю, в случае надобности никого не затруднит аналогичным образом найти длину ребра 2) Найдём уравнения ребра Уравнения ребра Для проверки подставляем координаты точек 3) Найдём угол между сторонами С помощью обратной функции находим сам угол: 4) Найдём площадь грани Таким образом, площадь грани
Если получаются страшноватые числа, не обращайте внимания, обычная картина. Главное, не допустить ошибку в вычислениях. 5) Найдём угол Это стандартная задача, рассмотренная в Задаче 162 (пункт
«д»). Используем формулу: 6) Составим уравнение грани Таким образом: Для проверки можно подставить координаты точек 7) Как составить уравнения высоты пирамиды? Звучит грозно, решается просто. Уравнения высоты
Вектор нормали в рассматриваемой задаче работает «на всю катушку», и как только вам предложили найти площадь грани, составить уравнение грани или уравнения высоты – сразу «пробивайте» векторное произведение. 8) Длину высоты Результат громоздкий, поэтому позволим себе вольность не избавляться от иррациональности в знаменателе. Теперь пунктик потруднее: 9) Найдём основание высоты – точку Перепишем уравнения высоты в параметрической форме: Основание высоты, понятно, лежит в плоскости. Подставим параметрические координаты точки Кому-то покажется жестью, но на самом деле шифер :) Который шуршит. Полученное значение параметра подставим в координаты нашей точки: Сурово, но идеально точно. Я проверил. 10) Объём треугольной пирамиды в ангеме традиционно рассчитывается с помощью
смешанного произведения векторов: Таким образом, И тут уместно выполнить проверку, вычислив объем тетраэдра по школьной формуле 11) Составим уравнения медианы Уравнения медианы можно составить по двум точкам, но сначала (см. по ссылке, почему) лучше найти
направляющий вектор: Уравнения медианы составим по точке Заметьте, что уравнения с эстетической точки зрения лучше составить по точке 12) Составим уравнение плоскости, проходящей через прямую Увы, мы не знаем «вкусный» вектор нормали, и поэтому уравнение
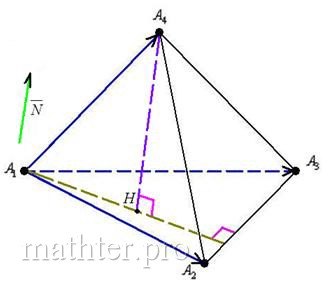
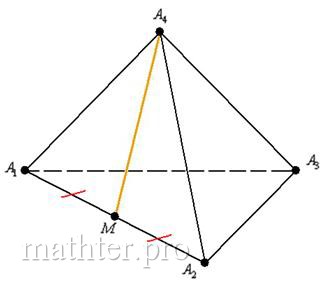
плоскости В качестве точки обязательно выбираем «одинокую» точку, которая не принадлежит прямой, в данном случае – это вершина Уравнение плоскости составим по точке Непременно проверяем, что координаты точек 13) Найдём угол между плоскостями Это типовая задача. Обозначим искомый угол через Осталось из уравнения Возиться с такими корнями смысла нет, поэтому сразу находим угол: От тупизны подальше за ответ таки лучше принять смежного соседа: 14) Выполним точный чертёж пирамиды С чего начать? Во-первых, нужно правильно изобразить декартову систему координат на клетчатой бумаге. Во-вторых, необходимо уметь строить точки в трёхмерном пространстве, о чём мы уже вспомнили, когда разбирали канонические уравнения прямой. И сейчас тема получает продолжение. Построим точку Теперь, в соответствии с отрицательной «зетовой» координатой, отмеряем 1 единицу вниз и тоже проводим пунктирную дорожку. Здесь и будет находиться
наша точка Для точки Аналогично строятся две другие точки. Заметьте, что вершина Теперь нужно разобраться в удалённости точек, а в этом как раз и помогут пунктирные линии. Немного включаем пространственное воображение и
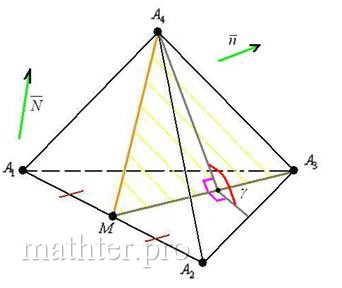
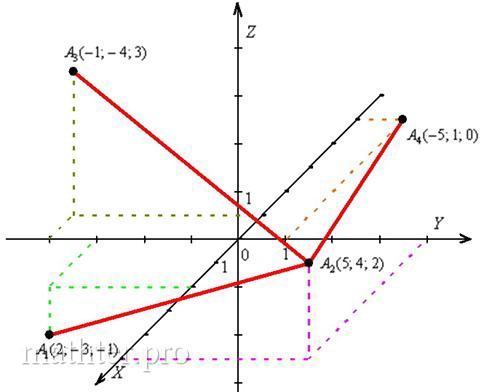
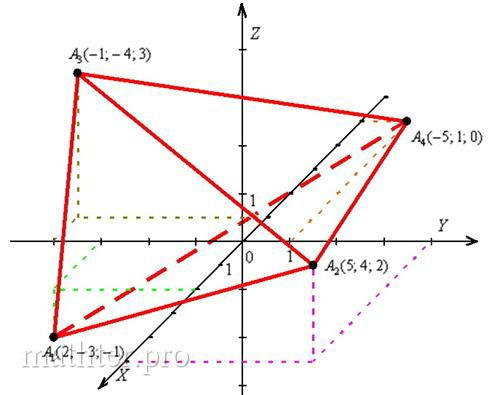
внимательно смотрим на ось Строим рёбра. Если есть сомнения, то сначала тонко-тонко прочерчиваем все 6 сторон и начинаем разбираться, какие рёбра видимы, а какие нет. Лучше начать от самой близкой точки Должен предостеречь, что так бывает далеко не всегда, одно ребро, например, может быть от нас скрыто. Не теряйте визуального восприятия пространства! Какие ещё стороны в зоне видимости? ВиднЫ рёбра Готово. Следует отметить, что чертеж-«конфетка» получается далеко не всегда. Бывает, что фортуна разворачивается задом. Так, грань пирамиды может полностью
или частично закрывать всё остальное (слева). Но самое скверное, когда перекрываются рёбра (справа). Тут сразу три ребра выстроились на одной прямой (правая верхняя прямая). В
подобной ситуации можно жирно прочертить накладывающиеся стороны разными цветами и ниже чертежа записать дополнительные комментарии о расположении
пирамиды. А можно поступить творчески – поменять оси местами (например, Существуют и более мелкие неприятности, например, одна из сторон пирамиды может наложить на координатную ось (а то и вовсе расположиться за ней). В конце решения следует выполнить Пункт 15, после чего желательно записать ответ, где по пунктам перечислить полученные результаты.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»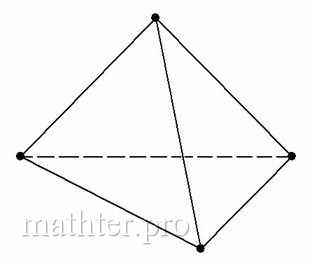
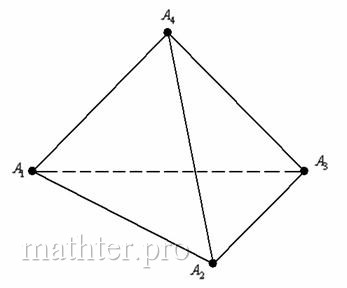 Если бегло просмотреть пункты условия, то легко заметить, что
там часто встречается грань
Если бегло просмотреть пункты условия, то легко заметить, что
там часто встречается грань 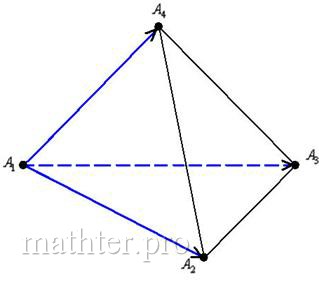 Решим эту
Решим эту 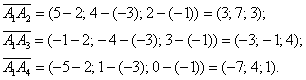
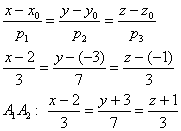
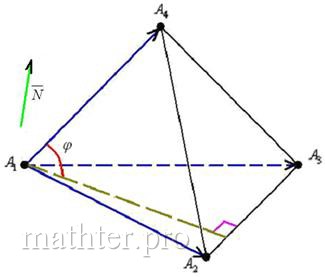
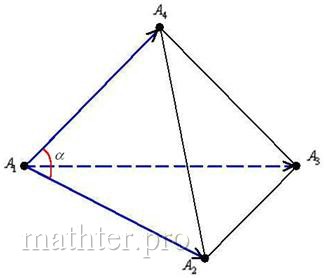 Перед вами обычный угол пространственного треугольника,
который рассчитывается как угол между векторами:
Перед вами обычный угол пространственного треугольника,
который рассчитывается как угол между векторами: 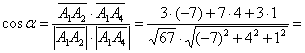
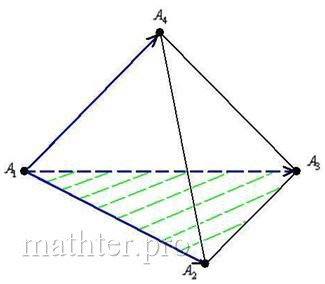 Площадь треугольника вычислим с помощью
Площадь треугольника вычислим с помощью 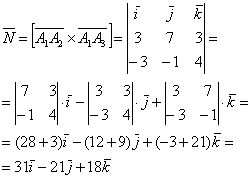
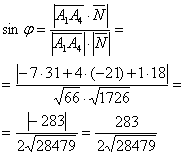
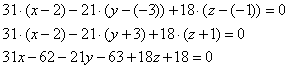
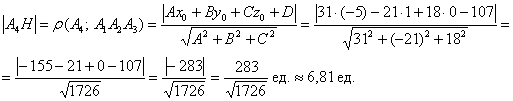
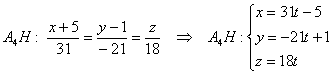
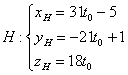 , или:
, или: 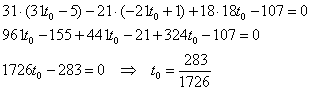
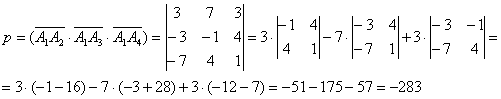
 По сравнению с
По сравнению с 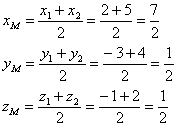
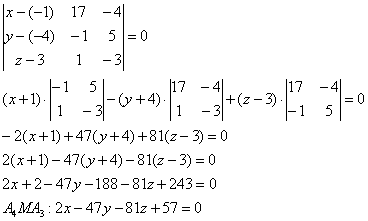
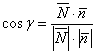 , где
, где 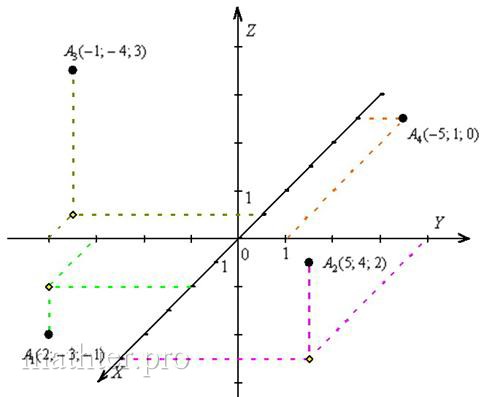
 6.1. Поверхности второго порядка
6.1. Поверхности второго порядка 5.6.7. Добро пожаловать в «реальные боевые условия»!
5.6.7. Добро пожаловать в «реальные боевые условия»!